Γιατί πανάκριβο ηλεκτρικό ρεύμα; – 1
2022/08/30
. . . . . . . . . . .
α. Εισαγωγή
Σίγουρα όλοι έχετε αγανακτήσει από τις πρόσφατες παράλογες καί τελείως αδικαιολόγητες χοντρές αυξήσεις της τιμής του ηλεκτρικού ρεύματος· άσε που, σε λίγο, καί θα πληρώνουμε όλοι μας τ’ άντερά μας, καί ρεύμα ΔΕΝ θα έχουμε!
. . . . . . . . . . .
[Ναί, πληρώνεις-δεν πληρώνεις, θα κόβεται κάποιες ώρες του 24ώρου – διότι δεν θα υπάρχει ικανή παραγωγή, να καλύψει τη ζήτηση. Ήδη κάποια πωλητικάντικα στόματα αρχίζουν να το ψιθυρίζουν αυτό. Καί, δυστυχώς, κανείς δεν αντιδρά ούτε κάν λεκτικώς… να πεί ότι:
«- Αφού σε πληρώνω ένα σκασμό λεφτά (καί χωρίς αντιρρήσεις), όχι μόνο θα μου παρέχεις ρεύμα συνεχώς (καί χωρίς αντιρρήσεις), αλλά θα γονατίσεις να μου …αγοράσεις καπνοσύριγγα, αν το απαιτήσω! Ξέρεις τί σημαίνει ‘καλοπληρωτής πελάτης’, ρέ παλιομ@λάκα; Ειδικά στην εποχή μας, όπου το μπαταχτσηλίκι είναι …θεσμός;
Καί το πώς θα καταφέρεις να έχεις συνεχή παραγωγή ρεύματος, δεν είναι δικό μου πρόβλημα. Σε τελευταία ανάλυση, βάλε όλο το υπουργικό συμβούλιο να γυρνάει δυναμό με τη μανιβέλλα. Τί με νοιάζει! Κόψε το λαιμό σου!»
. . . . . . . . . . .
Μάλλον αυτός ο λαός έχει πάθει σοβαρώτατη συλλογική εγκεφαλική βλάβη, μή αναστρέψιμη. Προφανώς το θεωρούν κι αυτό …φυσιολογικό, δηλαδή το να πληρώνουν καί να μην έχουν ρεύμα, όπως θεώρησαν φυσιολογική τη χονδροειδή απάτη των «εμβολίων».
(Οπότε, τί αγωνιζόμαστε κι εμείς απ’ τα ιστολόγια;!… Γιά ποιόν; Τέλος πάντων, άλλη ιστορία αυτό.) ]
. . . . . . . . . . .
Στο παρόν άρθρο, το ιστολογιάκι μας επιφυλάσσει (γιά σαρπράϊζ!) ένα πολύ γερό κλύσμα σε κάποιες κατηγορίες συνανθρώπων ( ; ) μας λωποδυτικού χαρακτήρος, περί των οποίων αρκετά παρακάτω στο κείμενο.
Σ’ αυτούς, συνιστώ:
- να βάλουν από τώρα βαζελίνη εκεί που ξέρουν, γιά να πονέσουν λιγώτερο,
- καί -επίσης από τώρα- να σβήσουν από τις άθλιες φάτσες τους τα τυχόν ειρωνικά «υπεράνω» χαμογελάκια· διότι, όταν κάποιος σ’ έχει στριμώξει στη γωνία καί σού ‘χει σπάσει τα παΐδια απ’ το ξύλο που σου ρίχνει, δεν γίνεται… δεν μπορείς αντικειμενικώς να είσαι άνετος καί χαμογελαστός.
Στην παρούσα «μονομαχία», άνετος καί χαμογελαστός μπορεί να είναι μόνον ο γράφων – κι όσοι συμφωνούν μαζί μου.
Ο λόγος, του γιατί πετάω το γάντι τόσο προκλητικά;
Τα καθαρώς επιστημονικά μου επιχειρήματα!
. . . . . . . . . . .
Βλέπετε, μέχρι τώρα αρκετοί έχουν κράξει τις σαχλοειδείς αυτές απάτες της «κλιματικής αλλαγής», της «πράσινης ανάπτυξης», καί των λοιπών πράσινων σκατών (προφανώς προερχομένων από «βήγκαν», δηλαδή από φυτοφάγους – καί οσονούπω κι εντομοφάγους)… που, μάλιστα, με αναγκάζουν να εγκαινιάσω από τώρα νέα ετικέττα αναρτήσεων, την: «πράσινα κόπρανα». (Διότι προβλέπω επερχόμενο βαρύ πρήξιμο των γεννητικών μου αδένων με τις διάφορες Γκρέτες, καί προετοιμάζω την άμυνά μου.)
[Ειρήσθω, ότι τα από καρδιάς εύσημα του γράφοντος απονέμονται στον Αρχαιοπτέρυγα· ο οποίος, χρόνια τώρα αγωνίζεται εναντίον της βλακείας της «πράσινης ανάπτυξης» με …ανεμογεννήτριες. Πάτε εγκαίρως στο μπλόγκι του να συλλέξετε απολύτως χρήσιμες πληροφορίες γιά το θέμα μας, γιά να προλάβετε να μή συμβεί στο ιστολόγιό του κανένα -χμ- «ατύχημα» ά λά Γκούγκλ… αν κι ο ιδιοκτήτης του έχει σταματήσει τις αναρτήσεις εδώ καί καιρό, καί το ιστολόγιό του παραμένει απείραχτο.]
Ωστόσο, τα επιχειρήματά τους, όσων μπήκαν στον κόπο ν’ αντιδράσουν, είναι στη χειρότερη περίπτωση (χειρότερη, γιά δημόσια αντιπαράθεση) ενστικτώδη καί συναισθηματικά («- Καταστρέφεται το δάσος!», «- Σκοτώνονται τα πουλιά στις ανεμογεννήτριες!»), καί στην καλύτερη περίπτωση οικονομικά. Γιά μένα, όλα τους είναι καί σωστά καί απολύτως σεβαστά, ειδικά τα τελευταία (αλοίμονο!… το πορτοφόλι μας ήδη το ξέρει πόσο σεβαστά είναι τα οικονομικά επιχειρήματα!…), πλήν όμως όλα τους είναι ανεπαρκή.
Γιατί;
Διότι το κάθε τσιράκι της «πράσινης ανάπτυξης» θα σου κολλήσει στα μούτρα ότι δεν ξέρεις από τεχνολογία. (Άρα, δεν δικαιούσαι να μιλάς – καί να διακόπτεις το έργο της πρασινο-αναπτυξιακής καταστροφής. Καί δεν δικαιούσαι να προδικάζεις ότι μιά μέρα δεν θα έχεις τζάμπα ρεύμα, …«αρνητή» της μεγαλοψυχίας του γκουβέρνου! )
Ναί, αλλά εδώ, στο ημέτερον μπλόγκιον, όλ’ αυτά τα κοπρόσκυλα βρήκαν να ξυστούν στη γκλίτσα του τσοπάνη!… Ψώνισαν από σβέρκο, σου λέω!
Διότι, τις μέν διαμαρτυρόμενες «επιτροπές κατοίκων», είτε θα τις πάρουν με την ειρωνεία («- Τί ξέρουν οι χωριάτες από τεχνολογία;»), είτε θα τις πάρουν με το γλυκομίλητο παραμύθι (σε συνάξεις δημαρχαίων καί λοιπών κομματοσκυλικών «τοπικών παραγόντων» καί χειροκροτητών) – γιά τα (δήθεν) οικονομικά οφέλη, που (καί καλά!) θα έχει ο τόπος, γιά την «ανάπτυξη», καί λοιπές πίπες (αθάνατε Μάρκο ντέΣάντ!).
. . . . . . . . . . .
[Ναί, πώς;! Θα σπεύδουν στα χωριά μας οι τουρίστες, να δουν ανεμογεννήτριες, λες καί δεν ξανάδαν!
Θα λέει, δηλαδή (δείχνοντας τα κορφοβούνια), ο καφετζής παύλα ψήστης στην πλατεία της Άνω Ραχούλας: «- Τουρίστ! Τουρίστ! Χίαρ άνε-μό-γκεννήτρια! Γουΐντ τουρμπάϊν, γιού νόου; Α-νά-πτυ-ξη! Γκρόουθ!»…
…Καί θα ρέει άφθονο το τουριστικό συνάλλαγμα! (Ναί, αμέ! Απ’ αυτό το πλευρό να κοιμάστε! )
Η όλη φάση μου θυμίζει μιά παλιά ατάκα του Χάρρυ Κλύνν, που παρίστανε τον τσομπάνο Τραμπάκουλα, καί τάχαμου τον ρωτούσε ένας δημοσιογράφος, αν το χωριό έχει τουρισμό. Κι απαντάει ο Τραμπάκουλας με το αμίμητο: «- Έ; Τί να κάνουν οι τουρίστες στο χωριό πιδάκι μ’; Να δούν τ’ς νιερουφίδις;» ]
. . . . . . . . . . .
Στην αφεντιά μου, όμως, τί θα πούνε, που τα πτυχία τους τά ‘χω ανά πάσα στιγμή γιά τον καταστροφέα εγγράφων;
Πάμε, λοιπόν, να δώσουμε τη μάχη μας μέσα στο λημέρι του Μινώταυρου!…
…Καί να του πετάξουμε τα μάτια έξω!
. . . . . . . . . . .
β1. Πλαίσιο εργασίας καί βοηθήματα
Σε όσα ακολουθούν, θα προσπαθήσω να είμαι πολύ επεξηγηματικός, καί να κρατηθώ στο ελάχιστο δυνατό επίπεδο επιστημονικής δυσκολίας· στη χειρότερη περίπτωση, προσπαθήστε να θυμηθήτε λιγάκι τα Μαθηματικά Γυμνασίου-Λυκείου! (Θα βοηθάω κι εγώ, εννοείται.)
Ως συγγραφικά βοηθήματα, θα έχω:
- Τίς πανεπιστημιακού επιπέδου γνώσεις μου στο τρίπτυχο: Φυσική / Μαθηματικά / Τεχνολογία.
- Το λογιστικό φύλλο.
- Ό,τι βρώ στο Διαδίκτυο από αξιόλογες αναφορές, γιά όσα θέματα θίγω.
Μην ξεχνάτε, δέ, ότι απευθύνομαι σε αναγνώστες με όχι αναγκαστικά το ίδιο γνωσιακό υπόβαθρο με την αφεντιά μου.
Μή μου πεί, λοιπόν, κανείς εξυπνάκιας ότι δεν έχω κάνει πλήρη μελέτη, ή ότι μου λείπουν στοιχεία· διότι, εδώ, ούτε διδακτορική διατριβή εκπονώ, ούτε κάν πτυχιακή εργασία. Ούτε έμμισθος καί μόνιμος ερευνητής είμαι σε κάποιο πανεπιστημιακού επιπέδου ίδρυμα, ούτε πλήρως εξοπλισμένο εργαστήριο έχω στη διάθεσή μου, ούτε χρόνο γιά κάτι καλύτερο από πλευράς αναλυτικής συγγραφικής παρουσιάσεως… πολλώι δέ μάλλον ελεύθερο χρόνο να ψάχνω βάσεις δεδομένων παγκοσμίως γιά πανεπιστημιακού επιπέδου σχετικές με το θέμα εργασίες, ως βιβλιογραφική μου αναφορά. (Καί, ακόμη περισσότερο, ελεύθερο χρόνο να καθήσω να τις διαβάσω αυτές τις εργασίες!!!)
Ό,τι μπορώ κάνω – καί τα υπόλοιπα τ’ αφήνω σε όποιον νομίζει πως είναι ικανός να προχωρήσει καί στο παραπέρα.
[…Δυστυχώς, αυτοί που τους πρέπει καί μπορούν το παραπέρα, μέχρι τώρα δεν μίλησαν. Γιά κακή τους τύχη, όμως, αυτουνούς τους περιμένω με τον βούρδουλα – παρακάτω, στο κείμενο.]
Αυτά μπορεί το μαγαζί, αυτά προσφέρει. Καί σ’ όποιον αρέσουμε.
. . . . . . . . . . .
Ακόμη μία οφειλόμενη επισήμανση:
Το θέμα θα το προχωρήσω σταδιακά, κι όχι απότομα. Από μία απλή (κι απλοποιημένη) εισαγωγή, έως την περιγραφή της σύνθετης σημερινής πραγματικότητας των δικτύων της ηλεκτρικής ενέργειας. Όθεν, μην πεταχτεί κάποιος -όντως γνώστης του θέματος- καί μου πεί ότι δεν ανέφερα τον τάδε παράγοντα καί τον άλλον καί τον παράλλον. Να κάνουν υπομονή, καί …θα τους αναφέρω τους παράγοντες! Ας μην βιάζονται· προχωράμε με λογικά βήματα, όχι λογικά άλματα.
Οι όντως γνώστες του θέματος, όντως τα ξέρουν· καί …το ξέρω ότι τα ξέρουν!
(Κυρίως) Γιά τους λοιπούς αναγνώστες γράφεται το παρόν.
. . . . . . . . . . .
Τελειώνοντας, συστήνω ενθέρμως έλεγχο των γραφομένων μου κι από εσάς! (Κυρίως απ’ όσους-ες «τό ‘χετε» με τα Μαθηματικά καί τα λογιστικά φύλλα.) Μην τα δέχεστε έτσι, όσο σωστά καί να είναι.
Γιατί;
Γιά λόγους αρχών. Η καθαρά επιστημονική έρευνα πρέπει να υφίσταται διαρκή έλεγχο από τον κάθε ενδιαφερόμενο. Κι εδώ, μπορεί μέν να μην κάνω πλήρη (καί μ’ όλους τους κανόνες) επιστημονική έρευνα, πλήν όμως κάνω πράγματι επιστημονική έρευνα.
Τώρα, βέβαια, αν κάποιου δεν του αρέσουν τα γραφόμενά μου, τα θεωρεί ελλιπή, κτλ (καί γιατί όχι; δεν είναι υποχρεωτικό να συμφωνεί), ας κάνει αυτός κάτι άλλο, καλύτερο – σ’ επιστημονικό επίπεδο πάντα. Όχι σε φτηνατζήδικη προπαγάνδα εντυπώσεων στα ΜΜΕ καί στο Διαδίκτυο. Ούτε σ’ εξυπνακιαδισμούς.
Ήδη έχουμε αρκετό κωλόχαρτο· δεν έχουμε έλλειψη από δαύτο.
. . . . . . . . . . .
β2. Ελαφρά φυσικο-μαθηματική θεωρία
Στα επόμενα, θα χρησιμοποιήσουμε εικονοποιημένα αποσπάσματα από το λογιστικό φύλλο, καθώς καί τα γραφήματα που προκύπτουν· ώστε, να σας δείξω καθαρά αυτό που έχω να πω. Επίσης, θ’ αναγράψω τις συναρτήσεις που χρησιμοποίησα, ώστε να δοκιμάσετε κι εσείς τους υπολογισμούς (αν το επιθυμείτε).
Υπ’ όψιν, τα διαγράμματα που θα παρουσιάσω, θα είναι κάπως απλοϊκά, διότι προτιμώ να κρατήσω το επίπεδο δυσκολίας χαμηλά. Οι απαιτούμενες εξηγήσεις, όμως, θα δίδονται στο κείμενο.
. . . . . . . . . . .
i. Μία πηγή εναλλασσομένου ρεύματος
Το (μονοφασικό) εναλλασσόμενο ηλεκτρικό ρεύμα, αυτό που έχουμε στα σπίτια μας από τους στύλους με τα σύρματα, έχει -εξελισσόμενο στον χρόνο- τη μορφή ημιτόνου (δές κι εδώ – ημίτονο / συνημίτονο, sine / cosine, βγάζουν ακριβώς την ίδια καμπύλη, αλλά μετατοπισμένη με «διαφορά φάσεως» 90 μοιρών, άλλως π/2.)
[Επειδή, όμως, υπάρχουν καί (νύν καί …τέως) ζωηροί αμφισβητίες μαθητές, που θα ρωτήσουν αν το εναλλασσόμενο ρεύμα μπορεί να παραχθεί καί σε άλλες κυματομορφές, πλην ημιτονοειδούς (πχ σε τετραγωνικούς παλμούς, σε τριγωνική, κτλ), η απάντηση είναι «ναί». Αλλά, στην πράξη, στους σταθμούς ηλεκτροπαραγωγής, έχει επικρατήσει η ημιτονοειδής. (Γιά λεπτομέρειες -γιατί; πώς;-, ρωτήστε ηλεκτρολόγους μηχανικούς· αρκεί να γνωρίζετε καλούτσικα Μαθηματικά Λυκείου, καί παραπάνω.)
Όμως, όσοι-ες πάτε ακόμη σχολείο, μην ρωτάτε τους δασκάλους σας πράγματα εκτός ύλης! Διότι ένα γνωστό προσώπατο -ονόματα δέν λέμε, υπολήψεις δέν θίγουμε!- ρωτούσε κάποτε τους δασκάλους του: «- Καί πού το ξέρεις εσύ, ότι δύο καί δύο κάνουν τέσσερα;», με αποτέλεσμα να το πετάνε έξω απ’ την τάξη! ]
Γιά το ημίτονο, ας δούμε:
- τις αριθμητικές τιμές του
- τη μορφή του
μέσα σε μία περίοδο, που θεωρητικώς (καί στο δημόσιο ηλεκτρικό δίκτυο της Ελλάδας) κρατάει 1/50 του δευτερολέπτου, δηλαδή 20 χιλιοστά του δευτερολέπτου – 20 msec. Σημειώστε, ότι η περίοδος στα Μαθηματικά αναγράφεται ως 2*π ( = 6.28, καί κάτι ψιλά). Πρακτικώς, βεβαίως (κι επειδή καμμία διάταξη ηλεκτροπαραγωγής δεν είναι μαθηματικώς τέλεια – πχ ποιά ρόδα αυτοκινήτου είναι μαθηματικώς τέλειος κύκλος; ), η φυσική περίοδος του ρεύματος έχει ένα σφάλμα προς τα πάνω, ή προς τα κάτω.
Ο αριθμητικός πίνακας, που δίνει τις τιμές του ημιτόνου σε κομμάτια ανά ένα εικοστό της περιόδου (δηλαδή σε «βήματα» του ενός msec), είναι ο εξής:
Επεξηγήσεις:
- Ο κόκκινος αριθμός πάνω αριστερά, είναι ο 2*π.
- Ο μπλέ, από κάτω του, είναι ο (2*π)/20. (Δηλαδή, το «βήμα» της αυξήσεως της περιόδου του ρεύματος ανά ένα msec.)
- Η στήλη B είναι ο πολλαπλασιαστής του μπλέ αριθμού,
- καί το εξαγόμενο το βλέπουμε στη στήλη D. (Δηλαδή: D8 = B8*$D$3, κτλ.)
- Η στήλη F υπολογίζει τα ημίτονα: F8 = sin(D8), κτλ.
- Η στήλη L είναι τα αντίστοιχα «τετράγωνα» των τιμών των ημιτόνων που βρήκαμε: L8 = F8^2, κτλ.
Η στήλη L χρειάζεται γιά να υπολογίσουμε τη λεγόμενη τιμή rms (root mean square), η οποία είναι το μέτρο ισχύος γιά το εναλλασσόμενο ρεύμα. Η rms είναι η ρίζα του μέσου όρου του αρθοίσματος των τετραγώνων, καί δίδεται -στον πίνακά μας- από τον τύπο: =sqrt(sum(L7:L26)/20). Εδώ βγαίνει 0.707 (καί κάτι ψιλά), όπως ακριβώς προβλέπεται θεωρητικώς. (Δες καί το σχετικό σχήμα στον σύνδεσμο της Γουΐκι.)
Οι απ’ ανάμεσα κενές στήλες υπάρχουν απλώς γιά ομοιομορφία με τους επόμενους αριθμητικούς πίνακες.
Το αντίστοιχο διάγραμμα είναι το εξής:

Πάμε, τώρα, στις…
. . . . . . . . . . .
ii. Δύο πηγές εναλλασσομένου ρεύματος
Προκύπτει το πρακτικό πρόβλημα: εάν δεν επαρκεί η ισχύς (γιά να καλύψεις τη ζήτηση) από μία πηγή (δηλαδή, εργοστάσιο) ηλεκτροπαραγωγής, τί κάνεις; Προφανώς ρίχνεις στην κατανάλωση ισχύ κι από μία δεύτερη πηγή.
Εδώ, όμως, αρχίζουν τα προβλήματα!… Διότι, άμα ρίξεις καί τις δύο πηγές στο ίδιο καλώδιο, θα γίνει χαμός! (Προσέξτε: ΔΕΝ αναφέρω αν οι πηγές αυτές είναι ανεμογεννήτριες, ή πυρηνικά εργοστάσια· ό,τι καί να είναι, το αποτέλεσμα προκύπτει ακριβώς το ίδιο: μπάχαλο!)
Βλέπετε, η Φυσική είναι Φυσική – καί δεν αστειεύεται. Σε δύο (ή περισσότερα) «συμπλέοντα» κύματα, λοιπόν, παρεμβαίνει η λεγόμενη αρχή της υπέρθεσης (ή επαλληλίας) των κυμάτων (σύνδεσμος με πολύ φτωχό περιεχόμενο στα Ελληνικά, – σύνδεσμος στα Αγγλικά), που λέει ότι το συνολικό κύμα είναι (ανά πάσα στιγμή) το άθροισμα των επί μέρους κυματομορφών, που το αποτελούν.
Τί σημαίνει αυτό στην πράξη; σημαίνει ότι το συνολικό ρεύμα δύο πηγών εναλλασσομένου (στο ίδιο καλώδιο) παράγει ισχύ είτε μεγαλύτερη απ’ ό,τι πρέπει, είτε μικρότερη απ’ ό,τι πρέπει! (Έως μηδενική!!!)
. . . . . . . . . . .
Θα δούμε τί συμβαίνει σε τέσσερεις περιπτώσεις, καί δύο υποθετικά πρακτικά παραδείγματα. Οι τέσσερεις περιπτώσεις είναι η υπέρθεση δύο ημιτονοειδών κυμάτων με καθυστέρηση («διαφορά φάσεως») του δεύτερου σε σχέση με το πρώτο:
- μηδενική (σ’ αυτή την περίπτωση, τα κύματα αυτά ονομάζονται «συμφασικά»),
- ένα τέταρτο της περιόδου (π/2, 0.250*Τ, 5 msec σε πραγματικό φυσικό μέγεθος),
- μία ημιπερίοδο (π, 0.500*Τ, 10 msec),
- τρία τέταρτα της περιόδου (3π/2, 0.750*Τ, 15 msec).
Θα διαπιστώσετε ιδίοις όμμασιν ότι: είτε υπάρχει καθυστέρηση, είτε όχι, δύο (ή καί περισσότερες) πηγές εναλλασσομένου ρεύματος στο ίδιο καλώδιο, είναι ο ορισμός της καταστροφής!
Χωρίς πολλά λόγια, καί με τους ορισμούς των βασικών συναρτήσεων στα κελλιά του λογιστικού φύλλου να παραμένουν οι ίδιοι (οι πρόσθετοι θα επεξηγηθούν), παίρνουμε:
. . . . . . . . . . .
ii.-1 Δύο ημίτονα συμφασικά
Ο αριθμητικός πίνακας:
- Η στήλη H είναι οι τιμές ημιτόνου του δεύτερου κύματος στην ίδια χρονική τιμή κάθε φορά με τις αντίστοιχες του πρώτου. (Βλέπουμε πως είναι ακριβώς ίδιες, πράγμα απολύτως λογικό.)
- Η στήλη J (επαλληλία) είναι, φυσικά, το άθροισμα των στηλών F καί H: J8=F8+H8, κτλ.
Το πρώτο ανησυχητικό συμπέρασμα, όμως, είναι πως η τιμή rms έχει διπλασιαστεί! Αυτό, πρακτικά σημαίνει πως, αν πάρουμε ρεύμα από τέτοιο καλώδιο, όλες οι -εκείνη τη στιγμή- τυχόν ενεργές συσκευές μας (ακόμη καί οι παλαιοί γλόμποι πυρακτώσεως) θα γίνουν βεγγαλικά! Δεν ξέρω, βέβαια, αν η προοπτική να χάσετε 3 έως 5 χιλιάρικα ευρώ (σε αξία ηλεκτρικών συσκευών) σας ενθουσιάζει, πάντως σας βεβαιώνω πως οι εκρήξεις των συσκευών σας θα είναι λίαν θεαματικές! Χόλλυγουντ σκέτο! Καρα-lol!!!
Το διάγραμμα:

Το δεύτερο ανησυχητικό συμπέρασμα, είναι πως καί οι μέγιστες / ελάχιστες τιμές του (συνολικού) κύματος έχουν διπλασιαστεί (2, -2), σε σχέση με το σκέτο ημίτονο.
Δηλαδή, μιλάμε γιά περίσσευμα ενέργειας, που όμως δεν ξέρουμε τί να το κάνουμε – διότι βρίσκεται εκτός ανεκτών αριθμητικών ορίων.
. . . . . . . . . . .
ii.-2 Δύο ημίτονα, καθυστέρηση π/2
Ο αριθμητικός πίνακας:
- Τα «κελλιά» στη στήλη H περιέχουν τον τύπο: H8=sin(D8-0.250*$D$1), κτλ.
- Το $D$1 είναι η τιμή 2*π· αλλά, τη δίνω με απόλυτη αναφορά, γιά να μην γίνεται υπολογισμός της κάθε φορά σε κάθε «κελλί».
Πάλι βλέπουμε ανεβασμένη την τιμή rms· αν κι όχι τόσο, όσο στην περίπτωση συμφασικών κυμάτων.
Το διάγραμμα:
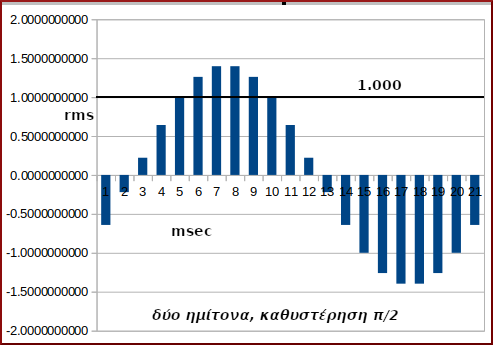
Πάλι ανεβασμένες (σε απόλυτες τιμές) καί οι ακραίες τιμές του συνολικού κύματος.
. . . . . . . . . . .
ii.-3 Δύο ημίτονα, καθυστέρηση π
Ο αριθμητικός πίνακας:
- Στήλη Η: H8=sin(D8-0.500*$D$1), κτλ.
Τα θερμά μου συγχαρητήρια!… Προκόψαμε! Ολική απώλεια ενέργειας!!!
Αυτό το ξέρουν καί οι (καλοί) μαθητές: πως, σε διαφορά φάσεως π, δύο ημιτονοειδείς κυματομορφές δίνουν άθροισμα τιμών μηδέν. Δεν είναι εκπληκτικό. (Στο πολύ περίπου, θα λέγαμε εναλλακτικώς καί πως σχηματίζεται ένα στάσιμο κύμα – δες καί τον αντίστοιχο αγγλόφωνο σύνδεσμο. Αν καί στο πολύ παραστατικό κινούμενο γραφικό, στον πρώτο σύνδεσμο της Γουΐκι, απεικονίζεται στάσιμο κύμα ως συμβολή δύο κυμάτων με διαφορά φάσεως όχι π.)
Το διάγραμμα:

Το απόλυτο μηδέν…
. . . . . . . . . . .
Υπ’ όψιν, το συγκεκριμένο διάγραμμα -καί μόνον αυτό- είναι επεξεργασμένο (με το πρόγραμμα επεξεργασίας εικόνας Gimp), γιά να δείχνει ακριβώς ό,τι προβλέπει η θεωρία. Διότι, το διάγραμμα που προέκυψε αυτομάτως από το λογιστικό φύλλο (το Calc του LibreOffice), μου έβγαζε -ως μή ώφειλε- δύο μεγαλούτσικες μή μηδενικές τιμές (μία θετική, μία αρνητική) στα 10.5 καί στα 20.5 msec. (Πού τις βρήκε, αγνοώ – τη στιγμή που όλες του οι τιμές πρέπει να είναι μηδενικές. Το λέει καί ο αριθμητικός πίνακας!)
Δυστυχώς, η ικανότητα των λογιστικών φύλλων να βγάζουν διαγράμματα, όπως ακριβώς τα θέλεις (κι όπως πρέπει), βρίσκεται ακόμη σε ψιλοτραγικώς χαμηλά επίπεδα! Έτσι, σας δίνω την πληροφορία, γιά να δοκιμάσετε κι εσείς την παραγωγή διαγραμμάτων στο δικό σας λογιστικό φύλλο, ΓΙΑ ΕΛΕΓΧΟ… γιά να μή λέει κανείς ότι «πειράζω» διαγράμματα, γιά να συμφωνούν με τις απόψεις μου.
[Αυτά τα κόλπα -«πείραγμα» τιμών των μετρήσεων, κτλ- μόνον οι μεγάλοι μπιστήμονες τα κάνουν! Όχι ημείς, οι διεθνώς άγνωστοι! Ημείς είμεθα πτωχοί, έντιμοι, καί δεν προτιθέμεθα να …διορθωθούμε! lol!!!
Δες, γιά παράδειγμα, πόσους θανάτους από κοροϊδοϊό προέβλεπε το πολλά βαρύ Ιμπήριαλ Κόλλετζ της αγγλίτσας. (Σύνδεσμος 1 με ευγενικό -αν καί μπαγιάτικο- κράξιμο. Σύνδεσμος 2 με ξέχεσμα, αν καί πολύ καθυστερημένο – σαν αντίδραση του Ράν-Τάν-Πλάν.)
Έπεσε έξω, το Ιμπήριαλ; Πολύ χοντρά!
Αυθαιρετούσε σε όσα ισχυριζόταν; Ναί!
Αναίρεσε; Ποτέ του!
Ζήτησε συγνώμην;
Τί λές, μωρέ Εργοδότη; «συγνώμη»; ναρκωτικά παίρνεις;
Ντράπηκε γιά όσα έλεγε;
…«Ντροπή»; τ’ είν’ αυτό; ]
Τα υπόλοιπα διαγράμματα του παρόντος, προέρχονται, φυσικά, από αυτόματη παραγωγή διαγράμματος από το λογιστικό φύλλο, με βάση -κάθε φορά- τη στήλη της επαλληλίας στον αντίστοιχο πίνακα· στο δέ σκέτο ημίτονο (πρώτη-πρώτη περίπτωση, απ’ όσες είδαμε), με βάση τη στήλη των τιμών ημιτόνου.
. . . . . . . . . . .
ii.-4 Δύο ημίτονα, καθυστέρηση 3*π/2
Ο αριθμητικός πίνακας:
- Στήλη Η: H8=sin(D8-0.750*$D$1), κτλ.
Η τιμή rms ξαναγίνεται μονάδα. Απόλυτα αναμενόμενο, αν σκεφτείς πως η καθυστέρηση κατά 0.750*Τ είναι συμμετρική της καθυστέρησης κατά 0.250*Τ.
Το διάγραμμα:

Επίσης συμμετρικό είναι καί το διάγραμμα με την περίπτωση καθυστέρησης κατά 0.250*Τ, μόνο που είναι μετατοπισμένο κατά ένα τέταρτο της περιόδου (5 msec) προς τ’ αριστερά. Αναμενόμενο.
. . . . . . . . . . .
ii.-5 Υποθετικό πρακτικό παράδειγμα 1
Είναι, όμως, στην πράξη τόσο μεγάλη η ασυμφωνία δύο ημιτονοειδών ρευμάτων επάνω στο ίδιο καλώδιο; να μη μπορούν κάν να συγχρονιστούν με διαφορά φάσεως μηδενική;
Όχι (συνήθως, όχι), αλλά ας δούμε ένα υποθετικό πρακτικό παράδειγμα, να δούμε τί πράγματι (μπορεί να) παίζει.
Ας υποθέσουμε ότι:
- Ξαφνικά -το καλοκαίρι- στα Ιωάννινα επικάθεται πολύ θερμός αέριος θύλακας με άπνοια, κι όλοι ανάβουν τα αίαρ κοντίσιον.
- Δεν επαρκεί η τροφοδοσία από το πλησιέστερο εργοστάσιο ηλεκτροπαραγωγής.
- Οι προμηθευτές ηλεκτρικής ενέργειας ρίχνουν στη ζήτηση των Ιωαννίνων ισχύ από το εργοστάσιο Αλιβερίου, έξω από τη Χαλκίδα.
- Τα δύο ρεύματα συναντιούνται στα Ιωάννινα, επάνω στα ίδια καλώδια πόλης.
Τώρα, το ηλεκτρικό ρεύμα μέσα σε καλό αγωγό κινείται περίπου με την ταχύτητα του φωτός, δηλαδή περίπου (καί κάτι λιγώτερο από) 300,000 km/sec (τριακόσιες χιλιάδες χιλιόμετρα το δευτερόλεπτο).
Εφ’ όσον η απόσταση Ιωάννινα-Χαλκίδα (Αλιβέρι) είναι περίπου 300 km σε ευθεία γραμμή…

…κι αν έχουμε αγωγό μεταφοράς τάσεως σε ευθεία γραμμή μεταξύ των δύο οικισμών, αυτό σημαίνει πως το ηλεκτρικό ρεύμα από το Αλιβέρι φτάνει στα Ιωάννινα με καθυστέρηση 1 msec (που χρειάζεται, γιά να διανύσει τα 300 km) σε σχέση με το τοπικό ρεύμα. (…Αν με κάποιον μαγικό τρόπο οι διακόπτες παροχής Ιωαννίνων καί Αλιβερίου κλείσουν μαζί σε απόλυτο συγχρονισμό.) Δηλαδή, με διαφορά φάσεως ένα εικοστό (1/20) της περιόδου των 50 Hz.
Οπότε, τα δεδομένα μας διαμορφώνονται ως εξής:
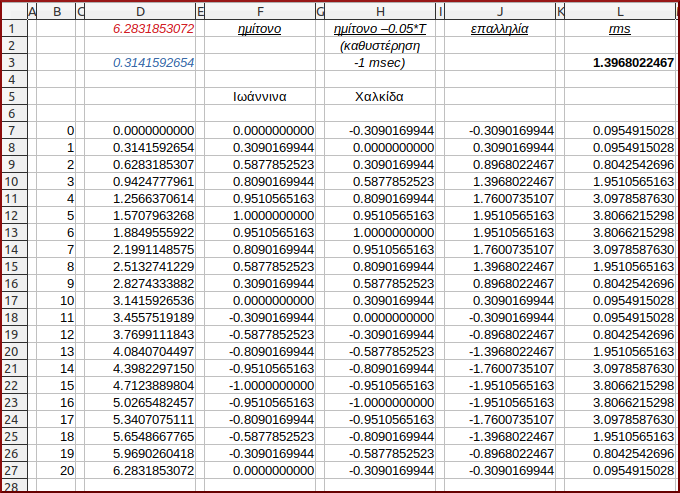
Ο αριθμητικός πίνακας:
- Στήλη Η: H8=sin(D8-0.050*$D$1), κτλ.
Το διάγραμμα:

Ο πίνακας καί το διάγραμμα εδώ δεν μας προσφέρουν κάποια καινούργια πληροφορία, απλώς (κατά κάποιο τρόπο) επιβεβαιώνουν το τί γίνεται με δύο απολύτως συμφασικά ρεύματα στο ίδιο καλώδιο. Μόνο που βλέπουμε πως αρκεί ένα msec, δηλαδή διαφορά φάσεως 0.050*Τ, ώστε να διαφοροποιηθεί η τιμή rms (προς τα κάτω) κατά 1.7%!
Σκεφθήτε, λοιπόν, τί γίνεται με μεγαλύτερες καθυστερήσεις! Το rms κατεβαίνει κι άλλο, η απώλεια ισχύος ανεβαίνει. (Θυμίζω ότι η δεκαπλάσια διαφορά φάσεως απ’ αυτήν που μόλις είδαμε, δηλαδή η ημιπερίοδος, δηλαδή η 0.500*Τ, μηδενίζει απολύτως τη διαθέσιμη ισχύ του καλωδίου!)
. . . . . . . . . . .
ii.-6 Υποθετικό πρακτικό παράδειγμα 2
Μεγαλύτερες καθυστερήσεις; Ναί. Υπάρχουν κι αυτές.
Από τα δεδομένα του τεχνικού φύλλου ενός συγκεκριμένου μοντέλου ανεμογεννήτριας (εδώ, σελίδα 7), βλέπουμε πως η διακύμανση συχνότητας του παραγομένου ρεύματος παίζει από 47 Hz έως 52.5 Hz.
Αυτό σημαίνει πως η περίοδος του παραγομένου ρεύματος της συγκεκριμένης ανεμογεννήτριας κυμαίνεται από 1/47 sec = 0.0212 sec = 2.12 msec, έως 1/52.5 sec = 0.0190 sec = 1.90 msec. Η διαφορά των δύο είναι: 2.12 – 1.90 = 2.2 msec, , δηλαδή 0.110*Τ (όπου Τ η θεωρητικώς βέλτιστη περίοδος των 20 msec).
Μ’ άλλα λόγια, κι αν υποτεθεί ότι:
- το άλλο κύμα έχει συχνότητα μία από τι δύο ακραίες της ανεμογεννήτριας,
- η ανεμογεννήτρια ξεκινάει ταυτόχρονα με το άλλο κύμα, όμως από την άλλη ακραία τιμή συχνοτήτων, αλλά
- μέσα σε μία μόλις περίοδο συγχρονίζεται σε συχνότητα (όχι σε φάση) με το άλλο κύμα,
τότε οδηγούμαστε στα εξής δεδομένα:
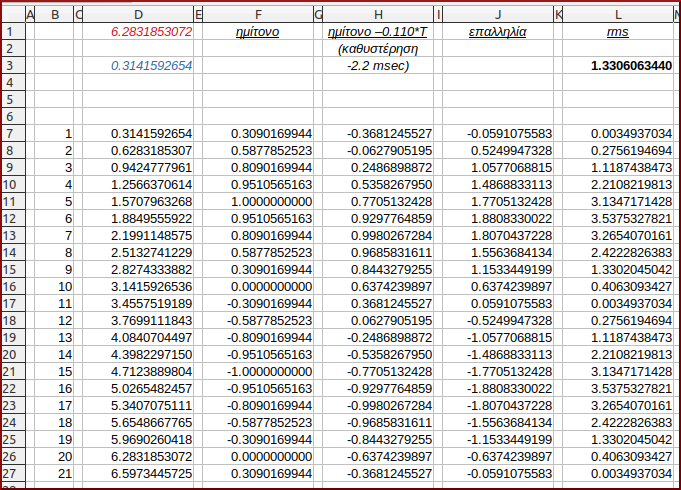
Ο αριθμητικός πίνακας:
- Στήλη Η: H8=sin(D8-0.110*$D$1), κτλ.
Το διάγραμμα:

Μ’ άλλα λόγια, έχουμε ακόμη μία πτώση της τιμής rms σε σχέση με την αμέσως προηγούμενη περίπτωση (άρα καί νέα απώλεια ισχύος), της τάξεως του 6.6%.
. . . . . . . . . . .
iii. Συμπεράσματα μέχρι στιγμής
Τα μέχρι στιγμής συμπεράσματα, είναι:
- Ποτέ δεν πρέπει να ρίχνουμε δύο (ή περισσότερα) εναλλασσόμενα ρεύματα πάνω στο ίδιο καλώδιο. Οδηγούμαστε είτε σε παραπανίσια (καί σχεδόν μή χρησιμοποιήσιμη) ισχύ, είτε σε (τελείως περιττές) απώλειες ισχύος.
- Αρκεί ένα χιλιοστό του δευτερολέπτου (1 msec) διαφορά φάσεως, γιά να έχουμε απώλειες, που μπορούμε κάλλιστα να τις αποκαλέσουμε μεγάλες. (Ακόμη καί το 1% απωλειών σε πανεθνικό επίπεδο, είναι πολύ σημαντικό. Είναι οικονομική αιμορραγία.)
Τώρα, βέβαια, όσα έγραψα μέχρι τώρα, οι ηλεκτρολόγοι μηχανικοί τα γνωρίζουν εδώ κι έναν αιώνα (καί κάτι ψιλά). Δεν περίμεναν εμένα, να τους τα υποδείξω. Επομένως, αντιμετωπίζουν την κατάσταση με άλλο τρόπο.
Πώς;
Η εξήγηση, παρακάτω.
. . . . . . . . . . .
Ωσάν υστερόγραφο στην ενότητα:
Θα ρωτούσε κάποιος (σκεπτόμενος) : «- Έ, ωραία! Αφού οι απώλειες προκύπτουν μαθηματικώς τόσο μεγάλες, γιατί να μην κάνουμε το εναλλασσόμενο ρεύμα να ταλαντώνεται μία φορά το δευτερόλεπτο, κι όχι 50; Αμέσως-αμέσως, οι απώλειες γίνονται πενήντα φορές μικρότερες – ανά μονάδα χρόνου, καί γενικώς!»
Σωστή σκέψη· πλήν όμως, τόσο η συχνότητα του χρησιμοποιούμενου εναλλασσομένου ρεύματος, όσο καί τα άλλα μεγέθη του (πχ τα 220 Volts, ή τα 150 kVolts των γραμμών μεταφοράς μεγάλης ισχύος / υπερυψηλής τάσεως), δεν είναι τυχαίοι αριθμοί. Προκύπτουν ως βέλτιστες αριθμητικές λύσεις κάποιων μαθηματικών τύπων, με συγκεκριμένη στόχευση (πχ ελαχιστοποίηση των απωλειών λόγωι ακτινοβολίας, στις γραμμές μεταφοράς μεγάλης ισχύος). Μόνο που δεν θα υπεισέλθουμε εδώ σε τέτοια θέματα.
Άρα, αφού τα Μαθηματικά μας είπαν: τόσο είναι η βέλτιστη συχνότητα, τόσο η βέλτιστη διαφορά δυναμικού, κτλ κτλ κτλ, οι καθιερωμένες παγκοσμίως αριθμητικές τιμές αυτών των μεγεθών δεν είναι φρόνιμο ν’ αλλαχτούν.
[Το μόνο υπαρκτό αλαλούμ σ’ αυτά τα πράγματα, είναι το εναλλασσόμενο ρεύμα, που κινεί τα τραίνα – καί δεν μπορώ να καταλάβω το γιατί δεν υπάρχει συμφωνία, τουλάχιστον παν-Ευρωπαϊκή. Στην γηραιά Ευρώπη υπάρχουν συνολικώς τουλάχιστον 3-4 διαφορετικές τιμές εναλλασσομένης τάσεως στις εναέριες γραμμές ηλεκτροδοτήσεως των τραίνων – άρα, γιά ποιά «Ευρωπαϊκή σύγκλιση» μιλάμε, ακόμη καί σε τόσο απλά πράγματα, όπως ένα πανευρωπαϊκό ταξίδι με τραίνο;
Δες κι εδώ, αναγνώστη μου, τον πίνακα στην πρώτη σελίδα κιόλας. Όχι πολύ βολική κατάσταση, θα έλεγα.]
. . . . . . . . . . .
(συνεχίζεται)






Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου