Επαν-ανακάλυψις Ηφαίστου – 2
 άμε να δούμε τί μας λένε οι ίδιες οι ημερομηνίες των (επαν-)ανακαλύψεων.
άμε να δούμε τί μας λένε οι ίδιες οι ημερομηνίες των (επαν-)ανακαλύψεων.
Τις τοποθετούμε στο λογιστικό φύλλο, καί βρίσκουμε τις διαδοχικές διαφορές τους (σε ημέρες), καθώς καί τον λόγο (δηλ. το κλάσμα) των διαφορών αυτών.
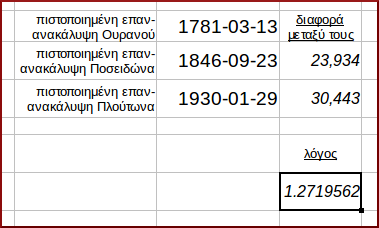
Παρά το ότι το αποτέλεσμα αυτό: (α) ήταν σχεδόν προφανές το τί σήμαινε, καί (β) μπορούμε να το χρησιμοποιήσουμε κατ’ ευθείαν, δεν το είδα αμέσως. (Ας όψεται αυτό το «σχεδόν»! ) Έτσι, πρώτα προχώρησα σε γεωμετρική διερεύνηση – καθ’ ό το ανεχόμενο φίδι προκύπτει από σχήμα.
Σκέφτηκα ότι ψάχνουμε γιά αριθμούς, όπως το 1.618, ή το 19.47. Ο πρώτος είναι ταυτόσημος της πεντάλφας, αλλά πενταγωνική συμμετρία δεν έβλεπα πουθενά. Ο δέ δεύτερος είναι η γνωστή «υπερδιαστατική» γωνία. Οπότε, σκέφτηκα να δω αν μπορώ να βρώ αναλογίες σε τρισδιάστατο σχήμα, κι αυτό ήταν η σφαίρα των «υπερδιαστατικών» πυραμίδων, παραλλαγμένη όμως. (Διότι οι υπερδιαστατικές πυραμίδες είναι ισοσκελείς, άρα δεν μας ενδιαφέρει ο λόγος 1:1.)
Συγκεκριμένα, να ξεκινάει η ουρά του φιδιού από τον πόλο σφαίρας, να πηγαίνει πρώτα σε γωνία 19.47 νότια (όχι βόρεια, όπως είναι στην ισοσκελή υπερδιαστατική πυραμίδα – σχήμα από αυτό το άρθρο), μετά να γυρίζει 120 μοίρες, μετά να πάει αντιδιαμετρικά (δηλ. το μεσαίο «τσάκισμα» του φιδιού να είναι 2 ακτίνες της σφαίρας), μετά πάλι 120 μοίρες πίσω, καί μετά στον άλλο πόλο της σφαίρας.
Δηλαδή, έτσι:

Πορεία ΑΒ – ΒΓ, δηλαδή τα ευθύγραμμα τμήματα α καί β. (Τα υπόλοιπα κομμάτια δεν απεικονίζονται.)
Από τους υπολογισμούς στο σχήμα, όμως, βγαίνει πως:
α = R*sqrt( (1-sinφ)^2 + cosφ^2 )
β = 2*R*cosφ*cos(30)
με φ = 19.47 μοίρες. Καί προκύπτει λόγος β/α = 1.4142029102 .
Είμαστε πολύ μακριά από τον λόγο των διαδοχικών διαφορών των (επαν-)ανακαλύψεων, άρα δεν είναι αυτό.
Τη λύση, όμως, έδωσαν τα σκέτα αριθμητικά δεδομένα.
Η προσεκτική μελέτη των άρθρων γιά τις επαν-ανακαλύψεις των τριών πλανητών πέραν του Κρόνου, έδειξε ότι αυτοί είχαν παρατηρηθεί καί πιό πρίν… καί μάλιστα, όχι μονάχα μία φορά! Μόνο που κατ’ εκείνες τις «προ»ανακαλύψεις, κανείς δεν κατάλαβε περί τίνος επρόκειτο.
Άρα, αφ’ ενός είχα στη διάθεσή μου περισσότερα αριθμητικά δεδομένα γιά εξέταση, αφ’ ετέρου…
…αλήθεια, εκείνο το έτος 1612, που ο Γαλιλαίος παρατήρησε τον Ουρανό (αν καί δεν κατάλαβε τί έβλεπε), έκανε μπάμ!
Βλέπετε, το πραγματικό «έτος μηδέν» της χρονολογίας μας είναι το 7 πΧ. Άρα, 1612+6 (διότι από το έτος 1 πΧ πάμε στο 1 μΧ, χωρίς να περάσουμε απ’ το μηδέν) = 1618!
[Μ’ αυτόν ακριβώς τον τρόπο ξέρω την ακριβή χρονιά της έκρηξης του ηφαιστείου της Σαντορίνης, χωρίς να χρειάζομαι χρονολογήσεις με άνθρακα-14, ή μελέτες καμμένων κλαδιών: 1618 + 7 = 1625 πΧ, με τη χρονολόγησή μας. Κάτι ξέραν καί οι ιερείς τότε, ποιό ήταν το «έτος αγκυρώσεως»…
…Καί βέβαια, μπορούμε πολύ εύκολα να πάμε μπρός, ή πίσω στον χρόνο, αν ξέρουμε τις αγκυρώσεις καί τις μαθηματικές σχέσεις, χωρίς να χρειάζεται να καταφύγουμε σε προφητείες· αλλ’ αυτά είναι άλλη ιστορία.]
Εδώ είμαστε!
Σαν κάτι να έλεγε στην ανθρωπότητα πως ήρθε ο καιρός να ξαναξυπνήσει…
Χαμογέλασα. Όμως, κι απ’ το 1612 μέχρι το 1781 η διαφορά είναι 169 χρόνια, δηλαδή λιγάκι παραπάνω από 161.8 . Το χαμόγελο εδώ έγινε πλατύτερο!
Πάμε, όμως, να δούμε τους σχετικούς πίνακες, με μία σημείωση: ότι στις 18 Φεβρουαρίου 1930 έγινε αντιληπτός ο Πλούτων (από την εξέταση των φωτογραφιών του τηλεσκοπίου), αλλά είχε φωτογραφηθεί οριστικά (γιά ανακάλυψη) στις 29 Ιανουαρίου.
Στους παρακάτω πίνακες, οι επιβεβαιωμένες παρατηρήσεις σημειώνονται με έντονα γράμματα.
Θέτουμε ως βάσεις αναφοράς μας τις ανακαλύψεις του Ουρανού, ο οποίος παρατηρήθηκε καί το 1690 από τον Φλάμστηντ, καί ανάμεσα στα έτη 175-1769 από τον Πιέρ Σάρλ λέ Μοννιέ. Άρα, θα δώσουμε πινακάκια χωριστά γιά κάθε περίπτωση, επειδή δεν χωράνε όλοι οι υπολογισμοί σ’ ένα.
i. «Ανακάλυψη» του Φλάμστηντ
Δίνουμε γιά αρχή καί τέλος του 1690:

Κάτι αρχίζει να φαίνεται, έ;
Παρατηρήστε, όμως, ότι η αναλογία 1/φ εμφανίζεται μεταξύ μή-επιβεβαιωμένων παρατηρήσεων.
ii. «Ανακάλυψη» του Πιέρ Σάρλ λέ Μοννιέ
Δίνω δύο πίνακες, γιά τα έτη 1750 καί 1769 χωριστά.


Παρατηρούμε εδώ ότι το φ εμφανίζεται σε σχέσεις μεταξύ επιβεβαιωμένων καί μή-επιβεβαιωμένων παρατηρήσεων. Ναί, όντως, κάπου πρέπει να κρύβεται η χρυσή αναλογία…
iii. Ανακάλυψη Χέρσελ

Το φ μεταξύ μή-επιβεβαιωμένων παρατηρήσεων.
Όμως, κάτι εξακολουθεί να μας διαφεύγει. Τί είναι αυτό το 1.27196… ;
Κι όμως, θα ‘πρεπε να το έχω δεί, αφού ξέρω καλά πρακτική αριθμητική! (Καί στο Στοίχημα, να δείς! ) Αφού 13×13=169, τότε το κάτι λιγώτερο του 1.3 επί τον εαυτό του, θα δίνει κάτι λιγώτερο του 1.69 . Καί ναί…

Εδώ είμαστε! Οι επιβεβαιωμένες επαν-ανακαλύψεις των πλανητών ακολουθούν τον παράγοντα της τετραγωνικής ρίζας του φ!…
Παρατηρήστε ότι στους πίνακες έβαλα την ημερομηνία της τελευταίας επιβεβαιωμένης φωτογράφησης του Πλούτωνα, κι όχι την επιβεβαίωση, στις 18 Φεβρουαρίου 1930. Αν την αλάξω (καί βάλω την 18η 2ου), η ακρίβεια μικραίνει λιγάκι. Ποιός ξέρει, στη συγκεκριμένη περίπτωση το Μάτριξ μας μιλάει με εικόνες (φωτογραφίες), να υποθέσω.
Πάντως, το βρήκαμε.
Τις τοποθετούμε στο λογιστικό φύλλο, καί βρίσκουμε τις διαδοχικές διαφορές τους (σε ημέρες), καθώς καί τον λόγο (δηλ. το κλάσμα) των διαφορών αυτών.

Παρά το ότι το αποτέλεσμα αυτό: (α) ήταν σχεδόν προφανές το τί σήμαινε, καί (β) μπορούμε να το χρησιμοποιήσουμε κατ’ ευθείαν, δεν το είδα αμέσως. (Ας όψεται αυτό το «σχεδόν»! ) Έτσι, πρώτα προχώρησα σε γεωμετρική διερεύνηση – καθ’ ό το ανεχόμενο φίδι προκύπτει από σχήμα.
Σκέφτηκα ότι ψάχνουμε γιά αριθμούς, όπως το 1.618, ή το 19.47. Ο πρώτος είναι ταυτόσημος της πεντάλφας, αλλά πενταγωνική συμμετρία δεν έβλεπα πουθενά. Ο δέ δεύτερος είναι η γνωστή «υπερδιαστατική» γωνία. Οπότε, σκέφτηκα να δω αν μπορώ να βρώ αναλογίες σε τρισδιάστατο σχήμα, κι αυτό ήταν η σφαίρα των «υπερδιαστατικών» πυραμίδων, παραλλαγμένη όμως. (Διότι οι υπερδιαστατικές πυραμίδες είναι ισοσκελείς, άρα δεν μας ενδιαφέρει ο λόγος 1:1.)
Συγκεκριμένα, να ξεκινάει η ουρά του φιδιού από τον πόλο σφαίρας, να πηγαίνει πρώτα σε γωνία 19.47 νότια (όχι βόρεια, όπως είναι στην ισοσκελή υπερδιαστατική πυραμίδα – σχήμα από αυτό το άρθρο), μετά να γυρίζει 120 μοίρες, μετά να πάει αντιδιαμετρικά (δηλ. το μεσαίο «τσάκισμα» του φιδιού να είναι 2 ακτίνες της σφαίρας), μετά πάλι 120 μοίρες πίσω, καί μετά στον άλλο πόλο της σφαίρας.
Δηλαδή, έτσι:

Πορεία ΑΒ – ΒΓ, δηλαδή τα ευθύγραμμα τμήματα α καί β. (Τα υπόλοιπα κομμάτια δεν απεικονίζονται.)
Από τους υπολογισμούς στο σχήμα, όμως, βγαίνει πως:
α = R*sqrt( (1-sinφ)^2 + cosφ^2 )
β = 2*R*cosφ*cos(30)
με φ = 19.47 μοίρες. Καί προκύπτει λόγος β/α = 1.4142029102 .
Είμαστε πολύ μακριά από τον λόγο των διαδοχικών διαφορών των (επαν-)ανακαλύψεων, άρα δεν είναι αυτό.
Τη λύση, όμως, έδωσαν τα σκέτα αριθμητικά δεδομένα.
Η προσεκτική μελέτη των άρθρων γιά τις επαν-ανακαλύψεις των τριών πλανητών πέραν του Κρόνου, έδειξε ότι αυτοί είχαν παρατηρηθεί καί πιό πρίν… καί μάλιστα, όχι μονάχα μία φορά! Μόνο που κατ’ εκείνες τις «προ»ανακαλύψεις, κανείς δεν κατάλαβε περί τίνος επρόκειτο.
- Ο μέν Πλούτων είχε φωτογραφηθεί άλλες τρείς φορές· στις 20 Αυγούστου 1909, καί στις 19 Μαρτίου καί 7 Απριλίου 1915.
- Ο Ποσειδών είχε παρατηρηθεί ακόμη κι απ’ τον Γαλιλαίο, με το τηλεσκοπιάκι του. Παρατηρήθηκε, δέ, καί στις 14 Ιουλίου του 1930, από τον Τζών Χέρσελ, γυιό του αστρονόμου που ανακάλυψε τον Ουρανό – κι επίσης βραβευμένου αστρονόμου.
- Όσο γιά τον Ουρανό, λέγεται πως φαίνεται καί με γυμνό μάτι (αλλά πρέπει νά ‘χει κανείς αετίσια όραση, υποθέτω), ο δέ πρώτος που σά-νά-νόμισε ότι τον είδε, ήταν ο Ίππαρχος.
Άρα, αφ’ ενός είχα στη διάθεσή μου περισσότερα αριθμητικά δεδομένα γιά εξέταση, αφ’ ετέρου…
…αλήθεια, εκείνο το έτος 1612, που ο Γαλιλαίος παρατήρησε τον Ουρανό (αν καί δεν κατάλαβε τί έβλεπε), έκανε μπάμ!
Βλέπετε, το πραγματικό «έτος μηδέν» της χρονολογίας μας είναι το 7 πΧ. Άρα, 1612+6 (διότι από το έτος 1 πΧ πάμε στο 1 μΧ, χωρίς να περάσουμε απ’ το μηδέν) = 1618!
[Μ’ αυτόν ακριβώς τον τρόπο ξέρω την ακριβή χρονιά της έκρηξης του ηφαιστείου της Σαντορίνης, χωρίς να χρειάζομαι χρονολογήσεις με άνθρακα-14, ή μελέτες καμμένων κλαδιών: 1618 + 7 = 1625 πΧ, με τη χρονολόγησή μας. Κάτι ξέραν καί οι ιερείς τότε, ποιό ήταν το «έτος αγκυρώσεως»…
…Καί βέβαια, μπορούμε πολύ εύκολα να πάμε μπρός, ή πίσω στον χρόνο, αν ξέρουμε τις αγκυρώσεις καί τις μαθηματικές σχέσεις, χωρίς να χρειάζεται να καταφύγουμε σε προφητείες· αλλ’ αυτά είναι άλλη ιστορία.]
Εδώ είμαστε!
Σαν κάτι να έλεγε στην ανθρωπότητα πως ήρθε ο καιρός να ξαναξυπνήσει…
Χαμογέλασα. Όμως, κι απ’ το 1612 μέχρι το 1781 η διαφορά είναι 169 χρόνια, δηλαδή λιγάκι παραπάνω από 161.8 . Το χαμόγελο εδώ έγινε πλατύτερο!
Πάμε, όμως, να δούμε τους σχετικούς πίνακες, με μία σημείωση: ότι στις 18 Φεβρουαρίου 1930 έγινε αντιληπτός ο Πλούτων (από την εξέταση των φωτογραφιών του τηλεσκοπίου), αλλά είχε φωτογραφηθεί οριστικά (γιά ανακάλυψη) στις 29 Ιανουαρίου.
Στους παρακάτω πίνακες, οι επιβεβαιωμένες παρατηρήσεις σημειώνονται με έντονα γράμματα.
Θέτουμε ως βάσεις αναφοράς μας τις ανακαλύψεις του Ουρανού, ο οποίος παρατηρήθηκε καί το 1690 από τον Φλάμστηντ, καί ανάμεσα στα έτη 175-1769 από τον Πιέρ Σάρλ λέ Μοννιέ. Άρα, θα δώσουμε πινακάκια χωριστά γιά κάθε περίπτωση, επειδή δεν χωράνε όλοι οι υπολογισμοί σ’ ένα.
i. «Ανακάλυψη» του Φλάμστηντ
Δίνουμε γιά αρχή καί τέλος του 1690:

Κάτι αρχίζει να φαίνεται, έ;
Παρατηρήστε, όμως, ότι η αναλογία 1/φ εμφανίζεται μεταξύ μή-επιβεβαιωμένων παρατηρήσεων.
ii. «Ανακάλυψη» του Πιέρ Σάρλ λέ Μοννιέ
Δίνω δύο πίνακες, γιά τα έτη 1750 καί 1769 χωριστά.


Παρατηρούμε εδώ ότι το φ εμφανίζεται σε σχέσεις μεταξύ επιβεβαιωμένων καί μή-επιβεβαιωμένων παρατηρήσεων. Ναί, όντως, κάπου πρέπει να κρύβεται η χρυσή αναλογία…
iii. Ανακάλυψη Χέρσελ

Το φ μεταξύ μή-επιβεβαιωμένων παρατηρήσεων.
Όμως, κάτι εξακολουθεί να μας διαφεύγει. Τί είναι αυτό το 1.27196… ;
Κι όμως, θα ‘πρεπε να το έχω δεί, αφού ξέρω καλά πρακτική αριθμητική! (Καί στο Στοίχημα, να δείς! ) Αφού 13×13=169, τότε το κάτι λιγώτερο του 1.3 επί τον εαυτό του, θα δίνει κάτι λιγώτερο του 1.69 . Καί ναί…

Εδώ είμαστε! Οι επιβεβαιωμένες επαν-ανακαλύψεις των πλανητών ακολουθούν τον παράγοντα της τετραγωνικής ρίζας του φ!…
Παρατηρήστε ότι στους πίνακες έβαλα την ημερομηνία της τελευταίας επιβεβαιωμένης φωτογράφησης του Πλούτωνα, κι όχι την επιβεβαίωση, στις 18 Φεβρουαρίου 1930. Αν την αλάξω (καί βάλω την 18η 2ου), η ακρίβεια μικραίνει λιγάκι. Ποιός ξέρει, στη συγκεκριμένη περίπτωση το Μάτριξ μας μιλάει με εικόνες (φωτογραφίες), να υποθέσω.
Πάντως, το βρήκαμε.
(επόμενο)
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου