ΜΕΡΟΣ Δ΄
Το Στομάχιον του Αρχιμήδη
ΤΟ ΣΤΟΜΑΧΙΟΝ ΕΙΝΑΙ ίσως η λιγότερο γνωστή από τις πραγματείες του Αρχιμήδη. Μέχρι την ανακάλυψη του Παλίμψηστου ήταν γνωστό μόνο ένα μικρό απόσπασμα της και αυτό όχι στην ελληνική γλώσσα, αλλά σε αραβική μετάφραση. Με την ανακάλυψη του Παλίμψηστου και την ανάγνωση του από τον Χά-ιμπεργκ ήρθε στο φως και ένα δεύτερο μικρό απόσπασμα (συγκεκριμένα, η εισαγωγή και το πρώτο θεώρημα) από την πραγματεία. Και τα δύο αποσπάσματα όμως είναι τόσο μικρά (στην έκδοση των Απάντων του Αρχιμήδη από τον Χάιμπεργκ δεν ξεπερνούν σε έκταση τις έξι σελίδες), ώστε ήταν αδύνατον να εξακριβωθεί ποιο ήταν το μαθηματικό περιεχόμενο της πραγματείας και για ποιο λόγο την έγραψε ο Αρχιμήδης. Έτσι, ελάχιστη σημασία δόθηκε στο Στομάχιον από τους ιστορικούς των μαθηματικών, οι οποίοι την αγνόησαν ή την περιφρόνησαν σαν ασήμαντη ή, τουλάχιστον, ακατανόητη.
Με τα μέχρι πρότινος δεδομένα, πιστευόταν ότι αντικείμενο του Στομαχίου ήταν να τοποθετηθούν δεκατέσσερα συγκεκριμένα επίπεδα σχήματα (τρίγωνα, τετράπλευρα και πεντάγωνα) με τρόπο ώστε να σχηματίζονται διάφορα άλλα γεωμετρικά σχήματα. Πιστευόταν δηλαδή ότι το Στομάχιον ήταν συναφές μ’ ένα παιδικό παιχνίδι, που αναφέρεται με την ίδια ονομασία από τους αρχαίους γραμματικούς, και στο οποίο το ζητούμενο ήταν να διατάσσονται μερικά ελεφάντι-να οστάρια πολυγωνικού σχήματος, ούτως ώστε να σχηματίζεται άλλοτε ένα ξίφος, άλλοτε μια περικεφαλαία, άλλοτε ένα πλοίο κ.λπ. Μάλιστα, η ονομασία «στομάχιον» προήλθε, κατά τη γνώμη κάποιων φιλολόγων, από τη στενοχώρια και την οργή που αισθάνεται κάποιος όταν παίζει αυτό το παιχνίδι, λόγω της μεγάλης δυσκολίας που παρουσιάζει. Αλλοι φιλόλογοι διατύπωσαν τη γνώμη ότι η ονομασία προήλθε από τον τύπο «όστομάχιον», που δηλώνει ακριβώς ένα παιχνίδι που παίζεται με οστά. Μια άλλη ονομασία που έχει προταθεί είναι «συντεμάχιον».
Αυτό ήταν το επίπεδο των γνώσεων μας για την πραγματεία του Αρχιμήδη μέχρι να καταπιαστούν εκ νέου με αυτή οι ερευνητές που μελετούν σήμερα το Παλίμψηστο. Από τη μελέτη προέκυψε ότι η παραδοσιακή εκδοχή (η οποία ούτως ή άλλως δεν ήταν πειστική, καθώς δύσκολα θα μπορούσε να δεχθεί κάποιος ότι ένας μαθηματικός του αναστήματος του Αρχιμήδη θα ήταν δυνατόν να ασχοληθεί και να αφιερώσει μια ολόκληρη πραγματεία σ ένα τέτοιο παιδικό παιχνίδι) βασιζόταν σε μια παρερμηνεία. Αυτό που στην πραγματικότητα επιδίωκε ο Αρχιμήδης δεν ήταν να συνενώσει δεκατέσσερα συγκεκριμένα κομμάτια ώστε να σχηματίζονται διαφορετικά σχήματα.
Το πρόβλημα που ήθελε να λύσει ήταν άλλο. Αυτό που προσπαθούσε να βρει ο Αρχιμήδης ήταν με πόσους τρόπους δεκατέσσερα επίπεδα σχήματα, στα οποία διαιρείται ένα τετράγωνο με βάση ένα προκαθορισμένο μοτίβο (ώστε το κάθε σχήμα να σχηματίζει ρητό λόγο προς το όλο τετράγωνο), μπορούν να συνενωθούν ώστε να σχηματιστεί και πάλι ένα τετράγωνο. Έτσι διατυπωμένο, το πρόβλημα γίνεται αμέσως ένα δύσκολο μαθηματικό πρόβλημα, το οποίο ανήκει μάλιστα στη συνδυαστική, έναν κλάδο των μαθηματικών που, όπως πιστεύαμε, είναι πολύ σύγχρονος. Αντικείμενο της συνδυαστικής είναι να υπολογιστεί με πόσους διαφορετικούς συνδυασμούς, με πόσους τρόπους δηλαδή, είναι δυνατόν να επιλυθεί ένα συγκεκριμένο πρόβλημα. Το Στομάχιον του Αρχιμήδη λοιπόν πραγματεύεται ένα πρόβλημα συνδυαστικής, και επομένως είναι η αρχαιότερη πραγματεία συνδυαστικής που γράφτηκε ποτέ.
Το κλειδί για να δοθεί αυτή η νέα ερμηνεία του Στομαχίου ήταν η ανάγνωση μιας λέξης (της λέξης «πλήθος»), την οποία ο Χάιμπεργκ δεν είχε μπορέσει να διαβάσει σωστά.
Είναι το Στομάχιον του Αρχιμήδη η αρχαιότερη πραγματεία συνδυαστικής που γράφτηκε ποτέ;
Η νέα ερμηνεία προτάθηκε από τον Ρέβιελ Νετζ (Reviel Netz), έναν από τους κύριους ερευνητές της ομάδας που μελετά το Παλίμψηστο. Ο Νετζ απευθύνθηκε σε μια ομάδα ειδικών στη συνδυαστική και τους ζήτησε να λύσουν το πρόβλημα, να υπολογίσουν δηλαδή με πόσους τρόπους τα δεκατέσσερα συγκεκριμένα σχήματα μπορούν να συνενωθούν για να σχηματιστεί ένα τετράγωνο. Το πρόβλημα τελικώς επιλύθηκε και βρέθηκε ότι -αν θεωρήσουμε ως ισοδύναμες τις λύσεις που προκύπτουν από περιστροφές και συμμετρίες- έχει 536 διαφορετικές λύσεις. Δεν ξέρουμε φυσικά αν ο Αρχιμήδης κατόρθωσε να βρει όλες αυτές τις λύσεις. Εξ όσων μπορούμε να συμπεράνουμε όμως από το γεγονός ότι έθεσε το πρόβλημα και ότι έγραψε μια ολόκληρη πραγματεία γι’ αυτό, καθώς και από τις γενικότερες γνώσεις που έχουμε για την αξία του Αρχιμήδη ως μαθηματικού, το πιθανότερο είναι ότι το κατόρθωσε.
Ιωάννης Χριστιανίδης
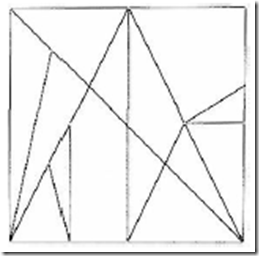
Στο σχήμα απεικονίζεται η σύνθεση του Στομαχίου που περιέχει η αραβική μετάφραση τμήματος
της πραγματείας του Αρχιμήδη.
Επισημαίνεται ότι η αναπαραγωγή του σχήματος στην έκδοση του Χάιμπεργκ (τ. 2, σ. 421) είναι
λανθασμένη (εμφανίζει το τετράγωνο να συγκροτείται από δεκαπέντε και όχι από δεκατέσσερα σχήματα). Το
ίδιο λάθος έχει μεταφερθεί στην ελληνική έκδοση των Απάντων του Αρχιμήδη (τ. Β; σ. 374), που επιμελήθηκε ο Ευάγγελος Σταμάτης.
ΒΙΒΛΙΟΓΡΑΦΙΑ
J. L. Heiberg (επιμ.): Archimedis opera omnia, cum commentariis Euticii, 3 τόμοι. Λειψία, 1910-1915. *R. Netz, F. Acerbi, N. Wilson: «Towards a Reconstruction of Archimedes Stomachion». Sciamus 5 (2004), 67-99. *H. Suter: «Der Loculus Archimedius oder Das Syntemachion des Archimedes. Zum ersten mal nach zwei arabischen Manuskripte der Koeniglichen Bibliothek in Berlin Herausgegeben una Obersetzt». Abhandlungen zur Geschichte der Mathematik 9 (1899), 491-499. * Αρχιμήδους Άπαντα, 3 τόμοι, επιμ. Ε. Σ. Σταμάτης. Αθήνα, 1970-1974. *
ΝΕΑ ΚΕΙΜΕΝΑ ΣΤΟ ΦΩΣ
Η ΠΡΟΤΑΣΗ-ΚΛΕΙΔΙ ΣΤΗΝ ΚΑΤΑΝΟΗΣΗ ΤΟΥ ΣΤΟΜΑΧΙΟΥ
Παραθέτουμε την πρόταση του κειμένου του Αρχιμήδη, η οποία περιέχει την κρίσιμη λέξη «πλήθος», την οποία δεν είχε μπορέσει να διαβάσει ο Χάιμπεργκ. Η ανάγνωση αυτής της πρότασης αποτέλεσε το «κλειδί» προκειμένου να μπορέσει ο Ρέβιελ Νετζ να προτείνει τη νέα ερμηνεία του Στομαχιού ως της αρχαιότερης πραγματείας περί συνδυαστικής.
Το κείμενο της πρότασης στην έκδοση του Χάιμπεργκ (τ. 2, σ. 416,15-18):
Έστι μέν ούν έξ αυτών ούκ ολίγων σχημάτων | ο.. διά τό
ν,.τον είναι \ εις έτερον τόπον του ίσον και ισογωνίου σχάματος
μετατιθεμε… \ και ετέ λαμβάνοντας.
Νεοελληνική απόδοση (με βάση τη μετάφραση του Ε. Σταμάτη):
Υπάρχουν μεν λοιπόν εξ αυτών όχι λίγα σχήματα … διότι ένα μέρος αυτών μπορεί να μετατεθεί στη θέση άλλου σχήματος το οποίο είναι ίσο και ισογώνιο.
Το κείμενο της πρότασης όπως έχει αποκατασταθεί μετά την ανάγνωση του Παλίμψηστου (Sciamus 5,2004,67-99, σ. 91):
Έστι μέν ούν έξ αυτών ούκ ολίγων σχαμάτων πλήθος, δια τό είλεν αυτός είναι εις έτερον τόπου του ίσου και ισογωνίου σχάματος μετατιθεμένου και ετέραν θέσιν λαμβάνοντος.
Νεοελληνική απόδοση (με βάση την αγγλική μετάφραση):
Υπάρχει μεν λοιπόν όχι μικρό πλήθος σχημάτων που σχηματίζονται από αυτά, διότι είναι δυνατόν να στραφούν (;) σε άλλη θέση ενός ίσου και ισογώνιου σχήματος, το οποίο έχει μετατεθεί για να λάβει άλλη θέση.
Η διαφορά ανάμεσα στις δύο εκδοχές του κειμένου είναι εμφανής.
Στην πρώτη εκδοχή το κείμενο φέρεται να σημαίνει ότι από έναν αριθμό αρχικών σχημάτων (πολυγώνων) είναι δυνατόν να σχηματισθούν διάφορα σύνθετα σχήματα, όπως συμβαίνει λ.χ. σ’ ένα κινεζικό παζλ (τάνγκραμ). Στη δεύτερη εκδοχή γίνεται λόγος για το πλήθος των σχημάτων που σχηματίζονται από τα αρχικά πολύγωνα. Αν λάβουμε τώρα υπ’ όψιν το διάγραμμα που συνοδεύει τη σωζόμενη αραβική μετάφραση (στο οποίο απεικονίζονται δεκατέσσερα μικρά πολύγωνα να συνδυάζονται μεταξύ τους ώστε να σχηματίζεται ένα τετράγωνο), μπορούμε να εικάσουμε ότι η λέξη «πλήθος» δηλώνει το πλήθος των συνδυασμών με τους οποίους από τα αρχικά πολύγωνα σχηματίζεται ένα και το αυτό σχήμα (στην προκειμένη περίπτωση ένα τετράγωνο).
(ΣΥΝΕΧΙΖΕΤΑΙ) https://spacezilotes.wordpress.com/

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου