Αν και έχει μετακινηθεί περισσότερο στο προσκήνιο για τους σημερινούς θιασώτες της «Νέας Εποχής», οι βασικές αρχές αυτού που είναι γνωστό ως Ιερή Γεωμετρία είναι ακόμα ελάχιστα κατανοητές. Σε αυτή τη σειρά άρθρων σε 3 μέρη, θα προσπαθήσουμε να απομυθοποιήσουμε το θέμα. Ας ξεκινήσουμε ορίζοντας την Ιερή Γεωμετρία...
Το λεξικό του Webster ορίζει το ιερό ως συνώνυμο με το ιερό. Εκτός από τους συνήθεις θρησκευτικούς συνειρμούς, μια γενικότερη έννοια που δίνεται είναι: «αφιερωμένη αποκλειστικά σε μία υπηρεσία ή χρήση (ως άτομο ή σκοπό)». Όταν, πριν από χρόνια, ασχολούμουν με το σχεδιασμό εκκλησιών, συνήθως σχεδιάζαμε ένα πολύ συγκεκριμένο δωμάτιο που ονομάζεται «σκευοφυλάκιο». Είναι επίσης γνωστό ως εσπερινός όπου φυλάσσονται τα ιερά σκεύη και τα άμφια που χρησιμοποιούνται στις λειτουργικές τελετές.
Το ιερό έχει λατινική ρίζα ίδια με αυτή της λέξης ιερός. Ο ιερός είναι το τελευταίο οστό στη σπονδυλική στήλη. Ο Webster λέει ότι είναι το «ιερό οστό» και αποτελείται από «το τμήμα της σπονδυλικής στήλης που συνδέεται άμεσα ή αποτελεί μέρος της λεκάνης και στον άνθρωπο αποτελείται από πέντε ενωμένους σπονδύλους». Θα δείτε αργότερα σε αυτό και σε επόμενα άρθρα πώς η σχέση με την ανθρώπινη ανατομία παίζει άμεσα στο θέμα μας.
Υπάρχει ένα άλλο ελάχιστα γνωστό συνώνυμο του ιερού, και αυτό είναι η λέξη μυστικό. Εδώ, υπονοεί κάτι εσωτερικό ή προορίζεται μόνο για λίγους να καταλάβουν για τη γεωμετρία. Ενώ αυτό μπορεί να ίσχυε στο παρελθόν, πιστεύω ότι είναι σημαντικό αυτή τη στιγμή στην ιστορία για περισσότερους ανθρώπους να κατανοήσουν τις συνέπειες του είδους της γεωμετρίας που ονομάζουμε ιερή. Πράγματι, μπορούμε να πούμε ότι η γη είναι ιερή καθώς εξαρτόμαστε από αυτήν για την ίδια την ύπαρξή μας.
Η λέξη γεωμετρία σημαίνει κυριολεκτικά «μετράω τη γη», ένας εύκολος ορισμός. Όλοι γνωρίζουμε τι σημαίνει να μετράς κάτι: το μήκος, το πλάτος και το ύψος του. Αλλά, αν μετράμε τη γη, είναι ολόκληρη η (άγια) γη ή μόνο ένα μικρό τμήμα του πλανήτη μας; Ή υπάρχει μια ευρύτερη έννοια στη λέξη Γη; Είναι ίσως πιο κατάλληλο στα συμφραζόμενά μας να χρησιμοποιήσουμε τη λέξη έδαφος, όπως στο «αγιασμένο έδαφος»; Πολλοί από εμάς χρησιμοποιούμε μερικές φορές το ρήμα γείωση που έχει σωματικές και ψυχολογικές επιπτώσεις. Στην πραγματικότητα, καθώς προχωράμε, νομίζω ότι θα δείτε ότι το σωματικό και το ψυχολογικό αρχίζουν να συγχωνεύονται μεταξύ τους.
Η γλώσσα των αριθμών και των συμβόλων
Οι διάφορες γλώσσες που ομιλούνται σε όλο τον κόσμο από την αρχή της καταγεγραμμένης ιστορίας δεν ήταν το πρώτο μέσο επικοινωνίας μεταξύ των ανθρώπων. Η αρχαιολογία μας δείχνει ότι ο πρώιμος άνθρωπος επικοινωνούσε πρώτα με τη χρήση διαφορετικών ειδών συμβόλων. Από τα σύμβολα προήλθαν οι αριθμοί, οι οποίοι είναι από μόνοι τους συγκεκριμένα είδη συμβόλων.
Γνωρίζουμε ότι στη μακρινή αρχαιότητα ο άνθρωπος άρχισε να χρησιμοποιεί έναν εικονογραφικό τρόπο για να επικοινωνήσει, είτε σκάλιζε σε πέτρα είτε απλώς ιχνηλατούσε με ένα ραβδί στην άμμο ή στο έδαφος. Καθώς γίναμε πιο εξελιγμένοι, σημαδεύτηκαν φύλλα παπύρου και αργότερα χαρτί από ξυλοπολτό. Τα σχήματα, τα γράμματα και οι αριθμοί δημιουργήθηκαν με μελάνι ή μπογιά χρησιμοποιώντας στυλό, μολύβι, πινέλο ή, αργότερα, γραφομηχανή. Σήμερα παράγονται με τη βοήθεια υπολογιστών. Ανεξάρτητα από το πώς γράφονται, οι αριθμοί και τα σύμβολα παραμένουν μια παγκόσμια γλώσσα.
Η Ιερή Γεωμετρία (ας την ονομάσουμε SG για συντομία) χρησιμοποιεί τόσο αριθμούς όσο και σύμβολα, αλλά με πολύ συγκεκριμένους τρόπους. Ενώ παρόμοια είδη γραφικών αναπαραστάσεων χρησιμοποιούνται σε σχέδια για την κατασκευή ενός κτιρίου ή σε μαθηματικές εξισώσεις, στο SG χρησιμοποιούνται με πολύ ακριβή τρόπο. Όπως λέει ο Webster, είναι «αφιερωμένα αποκλειστικά σε μία υπηρεσία ή χρήση...» Τα σύμβολα στο SG έχουν πολύ μοναδικές έννοιες, αν και, σύμφωνα με τον ορισμό μας για το ιερό ως μυστικό, αυτές οι έννοιες δεν είναι γενικά γνωστές.
Η γλώσσα των αριθμών και των συμβόλων (μιλάμε για καθαρούς αριθμούς εδώ, όχι για τη διαδικασία χρήσης αριθμών για υπολογισμούς) είναι η γλώσσα ορισμένων ικανοτήτων του ανθρώπινου εγκεφάλου που είναι διαφορετικές από εκείνες που χρησιμοποιούνται για την παραγωγή και την επικοινωνία με τον προφορικό λόγο. Όπως έχουμε σημειώσει, κάποιοι λένε ότι η γλώσσα των συμβόλων είναι η πιο πρωτόγονη μορφή επικοινωνίας. Αλλά με την SG αρχίζουμε να βλέπουμε μια εξαιρετικά εξελιγμένη συμβολική γλώσσα που υπερβαίνει τον προφορικό ή γραπτό λόγο.
Έχει αποδειχθεί ότι η γλώσσα είναι μια λειτουργία του αριστερού ημισφαιρίου του ανθρώπινου εγκεφάλου (τουλάχιστον για τους περισσότερους δεξιόχειρες). Έτσι είναι ο συνηθισμένος μαθηματικός υπολογισμός. Τα σύμβολα, από την άλλη πλευρά, ερμηνεύονται από τη δεξιά πλευρά του εγκεφάλου, όπως και οι εικόνες και άλλες οπτικές εικόνες. Όλοι γνωρίζουμε τη φράση «Μια εικόνα ίσον χίλιες λέξεις». Στο SG, ένα μόνο σχήμα ή μορφή μπορεί να έχει πολύ διακριτές έννοιες που θα χρειάζονταν πολλές σελίδες γραπτών λέξεων για να εξηγηθούν.
Το πρώτο μας καθήκον είναι να μάθουμε τη γλώσσα της Ιερής Γεωμετρίας.
Όπως παραπάνω, έτσι και κάτω
Ο πρωτόγονος άνθρωπος μπορούσε να δει τα αστέρια στον νυχτερινό ουρανό, ανεμπόδιστα από την αντανάκλαση των φώτων της πόλης από τα σύννεφα και τα στρώματα της ατμόσφαιρας. Ανακαλύψαμε ότι οι Αιγύπτιοι και οι Μάγια, μαζί με πολλούς άλλους αρχαίους πολιτισμούς, ήταν στενοί παρατηρητές του νυχτερινού ουρανού. Μόλις τώρα ανακαλύπτουμε ότι ήξεραν πράγματα που γνωρίζαμε μόνο με την έλευση του τηλεσκοπίου. Το πώς γνώριζαν όσα γνώριζαν για τους ουρανούς διερευνάται από τους ερευνητές. Παραμένει ένα μυστήριο, αλλά ίσως όχι για πολύ ακόμα.
Το πιο εντυπωσιακό παράδειγμα μιας αναπαράστασης που έγινε από τους αρχαίους στη γη και αντανακλά κάτι ορατό στον νυχτερινό ουρανό είναι η διάταξη των πυραμίδων στο οροπέδιο της Γκίζας, απέναντι από τον ποταμό Νείλο από το Κάιρο της Αιγύπτου.
Ο Robert Bauval και ο Adrian Gilbert στο βιβλίο τους The Orion Mystery του 1994 κάνουν μια καλή υπόθεση ότι οι τρεις πυραμίδες της Γκίζας, όταν φαίνονται από ψηλά, σχηματίζουν ένα αντίγραφο της θέσης των τριών αστεριών στη «ζώνη» του αστερισμού του Ωρίωνα. Σε ένα άλλο βιβλίο των Bauval και Graham Hancock που δημοσιεύθηκε δύο χρόνια αργότερα, το 1996, The Message of the Sphinx, η θεωρία επεκτείνεται για να δείξει ότι και άλλες πυραμίδες στο συγκρότημα ταιριάζουν επίσης στον αστερισμό του Ωρίωνα. Καθώς είμαστε τώρα σε θέση να υπολογίσουμε τις κινήσεις των αστεριών κατά τη διάρκεια χιλιάδων ετών με έναν υπολογιστή, η θέση των αστεριών στη ζώνη του Ωρίωνα σχηματίζει μια αντιστοιχία μόνο σε μια εποχή πολύ πριν οι πυραμίδες της Γκίζας ισχυριστούν από τους αιγυπτιολόγους ότι έχουν χτιστεί. (Πιο πρόσφατα, ο ερευνητής John Anthony West και ο γεωλόγος Robert Schoch έδειξαν ότι η διάβρωση γύρω από τη Σφίγγα προκλήθηκε από το νερό και όχι από τον άνεμο. Ήταν τουλάχιστον 10.000 χρόνια πριν που η έρημος στη βόρεια Αφρική ήταν ένα πλούσιο και καταπράσινο περιβάλλον με αρκετές βροχοπτώσεις για να εξηγήσει αυτή τη διάβρωση. Εάν η πρώτη ή Μεγάλη Πυραμίδα στη Γκίζα χτίστηκε περίπου την ίδια εποχή με τη Σφίγγα, η παλαιότερη ημερομηνία της αντιστοιχίας με τη ζώνη του Ωρίωνα έχει νόημα.)
Από το δημιουργικό έργο των Bauval, Gilbert και Hancock, άλλοι έχουν επεκτείνει την αναζήτηση και έχουν βρει πολλές αρχαίες τοποθεσίες σε όλο τον κόσμο που αναπαράγουν με κάποιο τρόπο αυτό που βλέπουμε στον νυχτερινό ουρανό ή χρησιμοποιούν τον ήλιο, τους πλανήτες και ορισμένα φωτεινά αστέρια ως βάση για τον προσανατολισμό των ανθρωπογενών κατασκευών τους. Το Στόουνχεντζ στη νότια Αγγλία είναι ίσως το πιο γνωστό παράδειγμα του τελευταίου. Αλλά υπάρχουν εκατοντάδες, αν όχι χιλιάδες περισσότερα τέτοια ερείπια.
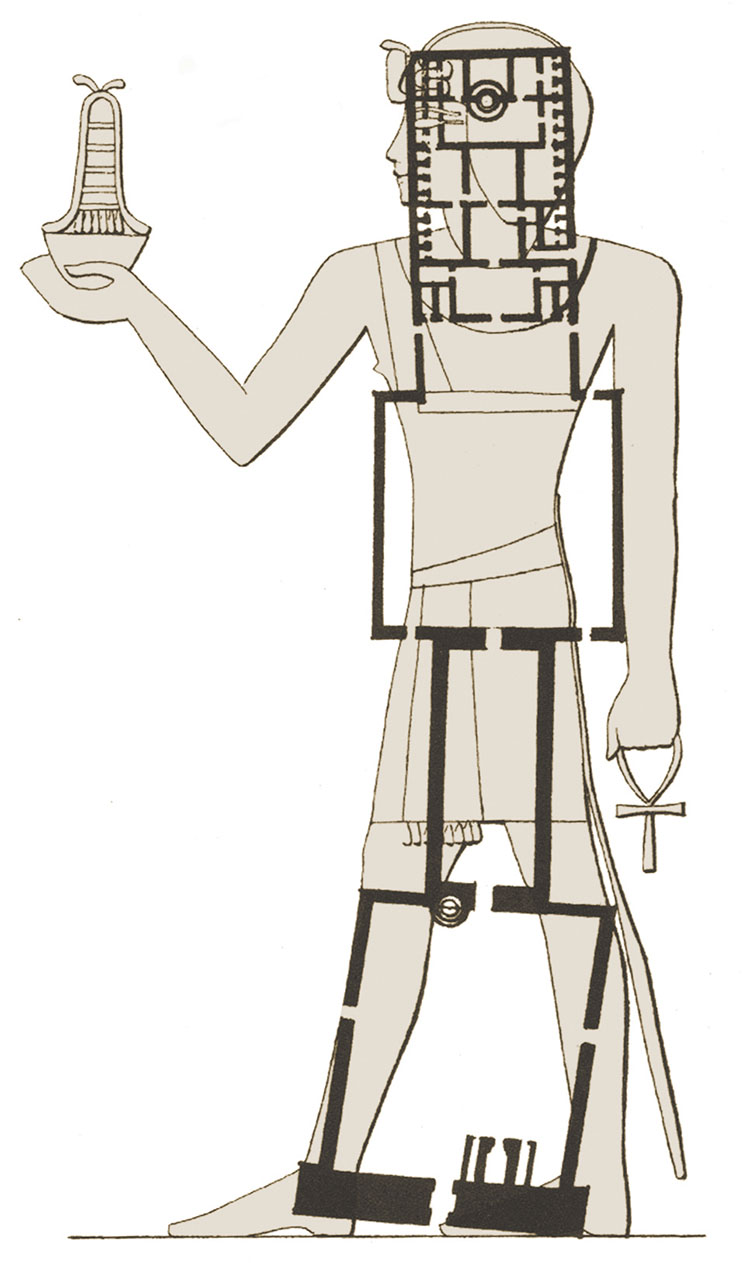
Σε μια άλλη κλίμακα μέτρησης, «όπως παρακάτω», διαπιστώνουμε ότι ορισμένες αρχαίες δομές αναμφίβολα διαμορφώθηκαν σύμφωνα με την ανατομία του ανθρώπου. Ο R.A. Schwaller de Lubicz έκανε μια 15ετή μελέτη της αρχιτεκτονικής του ναού του Λούξορ της Αιγύπτου. Το magnum opus του, The Temple of Man, δείχνει πώς η κάτοψη του Λούξορ και τα μέρη της αντικατοπτρίζουν το ανθρώπινο σώμα. Φτάνει μάλιστα στο σημείο να ταυτίσει διάφορους θαλάμους στο Ναό με τμήματα του εγκεφάλου.
Οι οικοδόμοι που συνδέονταν με τους Ναΐτες Ιππότες κωδικοποιούσαν εικόνες τμημάτων του ανθρώπινου σώματος μέσα στη γεωμετρία των μεγάλων γοτθικών καθεδρικών ναών της Μαρίας στη Γαλλία. Δεν είναι απλή σύμπτωση, όπως θα δούμε αργότερα. Και, «όπως παραπάνω», έχει αποδειχθεί ότι το συνολικό σχέδιο τοποθέτησης για αυτούς τους καθεδρικούς ναούς της Μαρίας φέρει μια εντυπωσιακή ομοιότητα με τη διαμόρφωση των αστεριών στον αστερισμό της Παρθένου, της Παναγίας.
Σε μοριακή κλίμακα, ο James Watson και ο Francis Crick δημοσίευσαν μια εργασία το 1953 στην οποία προσδιόρισαν το δομικό σχήμα του DNA ως διπλή έλικα. Πρόσφατα ανακαλύφθηκε ένα νεφέλωμα αερίου σε σχήμα διπλής έλικας που βρίσκεται σχεδόν κάθετα στην τεράστια μαύρη τρύπα στο κέντρο του Γαλαξία μας. Επίσης, σε αυτό που θα μπορούσαμε να ονομάσουμε μεσαίο έδαφος της ανθρώπινης κλίμακας μέτρησης, βλέπουμε τη διπλή έλικα που αντιπροσωπεύεται στην αρχιτεκτονική, και μάλιστα στην ιερή αρχιτεκτονική. Ο «Μαθητευόμενος Πυλώνας» μέσα στο παρεκκλήσι Rosslyn της Σκωτίας, που έγινε διάσημος από τον Κώδικα Ντα Βίντσι του Dan Brown, απεικονίζει ένα παράδειγμα στην επιφάνειά του μιας διπλής (ή ακόμα και τριπλής ή τετραπλής) έλικας σκαλισμένης σε πέτρα.
Όλα αυτά είναι σύμφωνα με το αρχαίο ρητό που αποδίδεται στον Ερμή τον Τρισμέγιστο και το γνωστό σύνθημα των ασκούμενων του ΓΓ, «ΟΠΩΣ ΠΑΝΩ, ΕΤΣΙ ΚΑΤΩ».
Ενσωμάτωση του λόγου f και του αριθμού 5
Η τρίτη τροφή του ανθρώπου
Κατά το σχεδιασμό κτιρίων για χρήση από τον άνθρωπο έχουμε πάντα κατά νου το μέγεθος και τις αναλογίες του ανθρώπινου σώματος, έτσι ώστε οι κατασκευές μας να σχετίζονται εύκολα με την ανθρώπινη λειτουργία. Η ρήση του μεγάλου 20ου αιώνα Ελβετός αρχιτέκτονας Le Corbusier, "Ένα σπίτι είναι μια μηχανή για τη ζωή," ισχύει με μια ευρύτερη έννοια σε όλους τους τύπους κατασκευής και χρήσεις. Ωστόσο, αυτό που μερικές φορές ξεχνάμε είναι ότι η ανθρώπινη λειτουργία είναι τόσο εξωτερική όσο και εσωτερική. Ναι, το σώμα περπατά και σέρνεται, τεντώνεται και φτάνει, ανεβαίνει και κατεβαίνει, κάθεται και ξαπλώνει. Αλλά αυτές είναι μόνο μερικές από τις εξωτερικές εκδηλώσεις της. Δεν πρέπει να ξεχνάμε την εσωτερική μας λειτουργία. Όχι μόνο ένα υγιές άτομο χρησιμοποιεί και τις πέντε φυσικές αισθήσεις, αλλά το σώμα, το μυαλό και τα συναισθήματα σχηματίζουν εντυπώσεις από μια συνολική πρόσληψη αυτών των αισθήσεων. Ακριβώς όπως από το φαγητό και το ποτό τρέφουμε το σώμα, και από τον αέρα που αναπνέουμε εξάγουμε οξυγόνο, για τη ζωή και την ύπαρξή μας, έτσι και οι εντυπώσεις αποτελούν ένα άλλο είδος τροφής. Στην πραγματικότητα, χωρίς την πρόσληψη και επεξεργασία των εντυπώσεων (ακόμα και όταν κοιμόμαστε), θεωρούμαστε νεκροί. Παρά την τεχνητή αναπνοή και την ενδοφλέβια σίτιση, ένας γιατρός εξακολουθεί να θεωρεί έναν ασθενή κλινικά νεκρό εάν δεν υπάρχουν εγκεφαλικά κύματα που εμφανίζονται στην οθόνη EEG.
Ακριβώς όπως τα φρέσκα τρόφιμα και ο καθαρός αέρας διατηρούν το σώμα μας υγιές, μπορεί να αποδειχθεί ότι ευδοκιμούμε καλύτερα με θετικές εντυπώσεις. Εκείνοι που σχεδιάζουν και κατασκευάζουν τα περιβάλλοντα διαβίωσης θα πρέπει να προσπαθήσουν να παράγουν περιβάλλον που οι κάτοικοι αντιλαμβάνονται ότι έχει ευχάριστες αναλογίες, χρώμα, υφή και κλίμακα πέρα από την απλή λειτουργική λειτουργικότητα. Οι άνθρωποι έχουν φυσικά σώματα που αξιολογούμε ως πιο ελκυστικά ή λιγότερο ελκυστικά αισθητικά, και είναι το ίδιο με τα κτίρια. Είναι ενδιαφέρον ότι εφαρμόζουμε πολλά από τα ίδια κριτήρια στις αντιλήψεις μας για την αρχιτεκτονική όπως και στις κρίσεις μας για την ανθρώπινη μορφή. Τόσο πολύ που η ευχάριστη και ακόμη και εμπνευσμένη αρχιτεκτονική μπορεί να αποδειχθεί ότι συσχετίζεται με συγκεκριμένες ιδιότητες του ανθρώπινου σώματος. Αυτός είναι αναμφίβολα ο λόγος για τον οποίο πολλοί από τους μεγάλους εικαστικούς καλλιτέχνες υπήρξαν επίσης σπουδαίοι αρχιτέκτονες.
Μετρώντας τον άνθρωπο με τη χρυσή τομή
Για να προχωρήσουμε με αυτή τη γραμμή μελέτης, ένα καλό μέρος για να ξεκινήσουμε είναι με τον λεγόμενο «Άνθρωπο του Βιτρούβιου» του Λεονάρντο ντα Βίντσι.
Ο Λεονάρντο ασχολήθηκε με το να δει την αρμονία στην ανθρώπινη ανατομία και αυτό το σκίτσο ανάμεσα στις πολλές ανατομικές μελέτες του είναι ίσως το καλύτερο παράδειγμα. Θέτει τις κατάλληλες αναλογίες για όλους τους μεταγενέστερους καλλιτέχνες και γλύπτες της ανθρώπινης μορφής. Και, ως απόδειξη της σοφίας του, μας δείχνει επίσης τη σχέση μεταξύ ανατομίας και καθαρής γεωμετρίας. Όπως λέει και η παροιμία, «Ο άνθρωπος είναι το μέτρο όλων των πραγμάτων». Επίσης, σύμφωνα με τη φράση οδηγό μας "Όπως πάνω, έτσι και κάτω", βλέπουμε τα μέρη του σώματος να εκφράζουν τις ίδιες αναλογίες με το σύνολο.
Οι αρχαίοι Αιγύπτιοι, οι Έλληνες, οι Ιάπωνες και ακόμη παλαιότεροι πολιτισμοί σε όλο τον κόσμο εδώ και πολύ καιρό προσδιόρισαν την αναλογία της περιφέρειας (C) ενός κύκλου προς τη διάμετρο του (D) ως C/D = 3.14159... Οι περισσότεροι από εμάς γνωρίζουμε από το μάθημα γεωμετρίας του γυμνασίου ότι αντιπροσωπεύουμε αυτόν τον αριθμό με το ελληνικό γράμμα p (Pi). Ονομάζεται «παράλογος» αριθμός, καθώς μπορεί να πραγματοποιηθεί σε άπειρο αριθμό δεκαδικών ψηφίων ανάλογα με το πόσο ακριβείς θέλουμε να είμαστε.
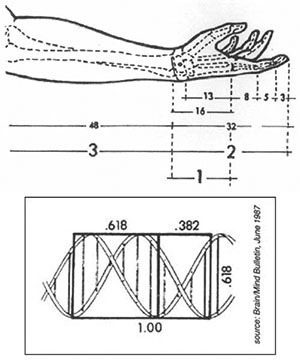
Μια άλλη σημαντική αναλογία, αλλά συνήθως δεν διδασκόμαστε στο γυμνάσιο, αντιπροσωπεύεται από το ελληνικό γράμμα F (Phi), όπου F = 1.618... (επίσης ένας «παράλογος» αριθμός). Προέρχεται από αυτό που εναλλακτικά ονομάζεται Χρυσή Τομή, Χρυσή Αναλογία ή Χρυσή Τομή - μια σχέση που ικανοποιεί τον κλασικό ορισμό της «αναλογίας της οποίας το σύνολο είναι στο μεγαλύτερο μέρος όπως το μεγαλύτερο μέρος είναι στο μικρότερο». Για όσους από εμάς έχουν γραφική κλίση, μπορούμε να δούμε αυτή την αναλογία σχεδιάζοντας ένα τμήμα γραμμής και διαιρώντας το σε δύο μέρη, a και b, με αναλογία 1: F όπως φαίνεται παρακάτω:
α = 1 β = Φ = 1.6180339887...
Σε αλγεβρικούς όρους, αντιπροσωπεύεται από την εξίσωση: (a + b)/b = b/a. Αυτή η σχέση μπορεί να προκύψει μόνο εάν b/a = 1.618..., η αριθμητική τιμή του F. Μπορούμε εύκολα να το δούμε αυτό αν εκχωρήσουμε μια τιμή 1 σε a και 1.618... στο β. Πάρτε μια αριθμομηχανή τσέπης και κάντε τα απλά μαθηματικά μόνοι σας. Όσο περισσότερα δεκαδικά ψηφία συμπεριλάβετε, τόσο πιο κοντά θα πλησιάσετε την τιμή του F.

Οι αρχαίοι χρησιμοποιούσαν αυτή τη χρυσή τομή για το σχεδιασμό των κτιρίων τους. Ο Παρθενώνας στην Αθήνα και η Μεγάλη Πυραμίδα στη Γκίζα έρχονται αμέσως στο μυαλό. Πέρα από την ίδια την αριθμητική τιμή και αγνοώντας για μια στιγμή ότι αυτή η αναλογία υποτίθεται ότι αντιπροσωπεύει μια ιδανικά ευχάριστη αναλογία (έτσι μας είπαν), ποια είναι η σχέση της με τον άνδρα / γυναίκα γενικά και, συγκεκριμένα, με το σκίτσο του Λεονάρντο για τον Άνθρωπο του Βιτρούβιου;
Πέντε, ο αριθμός του ανθρώπου
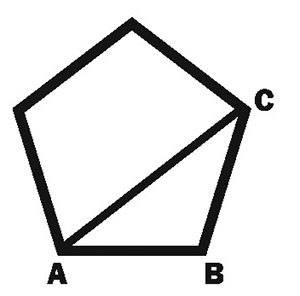
Χωρίς να υπεισέλθω σε άλλους υπολογισμούς σε αυτό το σημείο, επιτρέψτε μου να πω ότι ο αριθμός 5 παίζει σημαντικό ρόλο στη Χρυσή Τομή. Για να το δείξουμε εύκολα, ας δημιουργήσουμε μια κανονική φιγούρα 5 όψεων, ένα πεντάγωνο, με κάθε πλευρά να μετρά μία μονάδα όπως φαίνεται εδώ
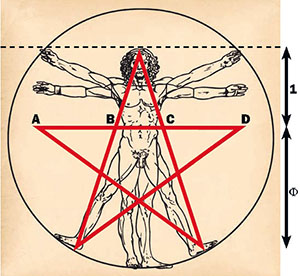
έτσι ώστε AB = BC = 1. Τώρα, αν συνδέσουμε οποιαδήποτε δύο αντίθετα σημεία με μια ευθεία γραμμή (για παράδειγμα, AC), αυτή η γραμμή θα μετρήσει 1.618..., την αριθμητική τιμή του F. Φυσικά, αν κοιτάξουμε τον άνδρα / γυναίκα σε μετωπική μορφή περιγράμματος, βλέπουμε πέντε εξαρτήματα που εκτείνονται από τον κεντρικό κορμό του σώματος: δύο χέρια, δύο πόδια και ένα κεφάλι. Αν πάρουμε τον Άνθρωπο του Λεονάρντο και περιστρέψουμε ελαφρώς τη θέση των χεριών προς τα κάτω, μπορούμε να επιγράψουμε ένα τέλειο πεντάγωνο γύρω από τη φιγούρα. Μέσα σε αυτό το πεντάγωνο μπορούμε να χαράξουμε ένα τέλειο πεντάγραμμο – ένα πεντάκτινο αστέρι, όπως φαίνεται παρακάτω σε ένα σκίτσο που αποδίδεται στον Αγρίππα. Είναι αυτονόητο ότι τόσο το πεντάγωνο όσο και το πεντάκτινο αστέρι έχουν μεγάλη σημασία, ειδικά στις Ηνωμένες Πολιτείες.
Έχουμε σε «πεντάδα» έναν αριθμό και γεωμετρικά σχήματα με βαθύ και πολυεπίπεδο νόημα. Ο ίδιος ο άνδρας και η ίδια η γυναίκα αντιπροσωπεύονται συμβολικά συνολικά από αυτόν τον αριθμό και από αυτά τα σχήματα. Και, για άλλη μια φορά, ισχύει το "As Above, So Below": έχουμε πέντε δάχτυλα σε κάθε χέρι και πέντε δάχτυλα σε κάθε πόδι. Το σύνολο αντηχεί στα μέρη. Και αυτό είναι μόνο η αρχή.
Πάνω είναι ένα σχέδιο επικάλυψης (όχι σε κλίμακα). Αν αποδώσουμε μια τιμή 1 στην απόσταση από τη γραμμή AD που μετράται κάθετα στην κορυφή του κεφαλιού του άνδρα, τότε, μετρώντας κάθετα προς τα κάτω από το AD στα κάτω δύο σημεία του πενταγράμμου στα δάχτυλα των ποδιών του άνδρα, διαπιστώνουμε ότι η απόσταση είναι 1.618... Επίσης, βρίσκουμε τις ακόλουθες αναλογίες: AD / AC = F , και AC / AB = F. Και πάλι, τα μέρη είναι ανάλογα με το σύνολο.
Κέντρο βάρους
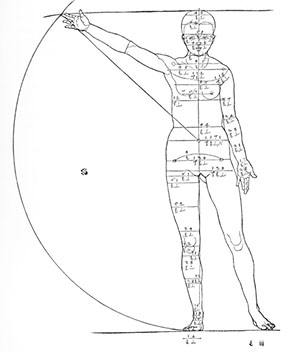
Τέλος, έχουμε το σκίτσο του Albrecht Dürer που δείχνει το ανθρώπινο σώμα διαιρούμενο με το F στον ομφαλό και διαιρεμένο στη μέση με τα γεννητικά όργανα:
Όταν γεννιέται ένα μωρό, ο ομφαλός χωρίζει το σώμα στο μισό. Καθώς το παιδί μεγαλώνει, οι σωματικές αναλογίες αλλάζουν έτσι ώστε τα πόδια να είναι μακρύτερα σε σχέση με τον κορμό. Μέχρι την ενηλικίωση, ο ομφαλός έχει μετακινηθεί προς τα πάνω (σε σχέση με το συνολικό ύψος του ατόμου) στη θέση του λόγου F όπως φαίνεται τόσο στα σχέδια da Vinci όσο και στα σχέδια του Dürer. Κάποιοι λένε ότι αυτό αντιπροσωπεύει την αρχή ενός ανθρώπινου όντος που ωριμάζει από μια φύση δυαδικότητας σε μια φύση ασύμμετρης αλλά αρμονικής αναλογικότητας. Είναι ενδιαφέρον να σημειωθεί ότι το επίπεδο του ομφαλού θεωρείται σε ορισμένες ανατολικές παραδόσεις ως το κέντρο βάρους ενός ατόμου και χρησιμοποιείται ως τέτοιο σε ορισμένες διαλογιστικές πρακτικές.
Η φύση εμφανίζει Phi, Fibonacci, &; Πέντε
Ο Leonardo Bigollo Fibonacci, γνωστός και ως Leonard da Piza (Pisano), ταξίδεψε στο Αλγέρι ως νεαρός άνδρας και έφερε πίσω στην Ευρώπη τη χρήση αραβικών αριθμών για να αντικαταστήσει το δυσκίνητο ρωμαϊκό σύστημα αρίθμησης. Από γεωμετρητές στο Αλγέρι έμαθε επίσης για διάφορες προσθετικές σειρές αριθμών που παράγονται από τη Χρυσή Αναλογία του phi.

Υπάρχουν πολλές ακολουθίες ακέραιων αριθμών που ονομάζονται προσθετικές σειρές (προοδευτικοί αριθμοί που δημιουργούνται προσθέτοντας τον πρώτο και τον δεύτερο αριθμό για να φτάσουν στον τρίτο αριθμό), αλλά μόνο μία τέτοια ακολουθία ταξινομείται από αυτό που είναι τώρα γνωστό ως σειρά Fibonacci: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181 και ούτω καθεξής. Το ενδιαφέρον είναι ότι όταν υπολογίζουμε την αναλογία μεταξύ κάθε αριθμού και αυτού ακριβώς πριν από αυτόν στη σειρά, όσο υψηλότερα πηγαίνουμε τόσο πιο κοντά φτάνουμε στην αριθμητική τιμή του phi. Για παράδειγμα, 5/3 = 1.666666...; 55/34 = 1,617647; και 987/610 = 1,6180327.
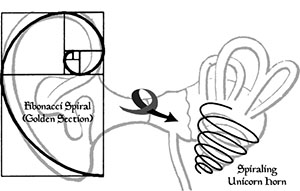
Λογαριθμικές σπείρες σειράς Fibonacci
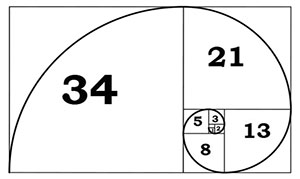
Από τη διαδοχή των αριθμών Fibonacci μπορούμε γεωμετρικά να παράγουμε ένα συγκεκριμένο είδος σπείρας. Ένας τρόπος για να γίνει αυτό είναι με την ένθεση συνεχώς αυξανόμενων μεγεθών περιστρεφόμενων ορθογωνίων 90 μοιρών διαιρούμενων με τετράγωνα σύμφωνα με την αναλογία phi και στη συνέχεια συνδέοντας τα σημεία όπου τα τετράγωνα χωρίζουν τις πλευρές των ορθογωνίων σε χρυσές αναλογίες με καμπύλες γραμμές που χαράσσουν το ένα τέταρτο ενός κύκλου. Οι προκύπτουσες περιοχές των τετραγώνων είναι στην ακολουθία της σειράς αριθμών Fibonacci, όπως φαίνεται παρακάτω:
Απλώς συμβαίνει να βλέπουμε μια τέτοια σπείρα Fibonacci να επαναλαμβάνεται ξανά και ξανά στη Φύση. Στην πραγματικότητα, ενώ η συμμετρία παρατηρείται συχνά στον κόσμο μας (για παράδειγμα, έχουμε δύο συμμετρικά τοποθετημένα χέρια, πόδια, μάτια, αυτιά, ρουθούνια κ.λπ.), υπάρχουν στην πραγματικότητα περισσότερα παραδείγματα της ασυμμετρίας της σειράς Fibonacci. Το πρόβλημα είναι ότι έχουμε ξεχάσει να τα ψάξουμε.
Η σειρά Fibonacci αντιπροσωπεύεται στη δομή πολλών ζωντανών οργανισμών και φυσικών διεργασιών, όπως η κατανομή των φύλλων σε ένα φυτό, τα σπειροειδή κοχύλια, τα πέταλα λουλουδιών, τα κάτω μαξιλάρια στους πρόποδες μιας γάτας, η πλανητική τροχιά της Αφροδίτης όπως φαίνεται από τη Γη, η κατανομή των σπόρων σε έναν κάκτο και σε έναν ηλίανθο, αλλαγές στην ακτινοβολία ενέργειας, η αναλογία αρσενικών και θηλυκών μελισσών σε μια κυψέλη, το μόριο DNA, το επιφανειακό μοτίβο των κώνων πεύκου, πολλαπλές αντανακλάσεις φωτός μέσω καθρεφτών, ο κοχλίας του ανθρώπινου αυτιού, το πρότυπο αναπαραγωγής κουνελιών, σπειροειδείς γαλαξίες, η πορεία ορισμένων αρπακτικών πτηνών που πετούν κάτω για να αρπάξουν τη λεία τους, και πολλά άλλα. Ακολουθούν εικόνες μερικών από αυτά τα παραδείγματα:
Ο αριθμός 5 στη φύση
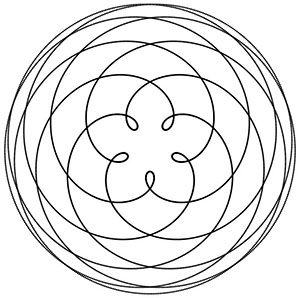
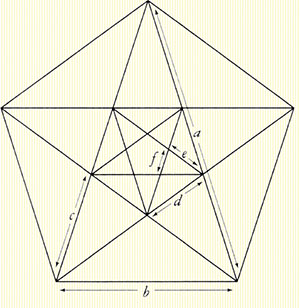
Δείξαμε παραπάνω ότι η αναλογία μεταξύ μιας διαγωνίου και μιας πλευράς ενός κανονικού πενταγώνου ισούται με phi. Συνδέοντας όλες τις γωνίες του πενταγώνου μπορούμε να εγγράψουμε ένα πεντάγραμμο αστέρι μέσα στο σχήμα του πενταγώνου. Στο παρακάτω σχήμα, θα παρατηρήσετε ότι μέσα στο πεντάγραμμο υπάρχει ένα άλλο, μικρότερο πεντάγωνο, και μέσα σε αυτό, επίσης, μπορούμε να γράψουμε ένα ακόμα μικρότερο πεντάγραμμο. Αυτό μπορεί να γίνει επ' αόριστον ανεβαίνοντας την κλίμακα σε μέγεθος (μακρόκοσμος) και κάτω στην κλίμακα σε μέγεθος (μικρόκοσμος).
Ένα συναρπαστικό χαρακτηριστικό των μηκών των γραμμών που χρησιμοποιούνται για την κατασκευή των αριθμών πενταγώνου/πενταγράμμου είναι ότι, καθώς προχωράμε από τη μεγαλύτερη στην επόμενη μικρότερη γραμμή (a προς b, b προς c, c έως d κ.λπ.), ο λόγος των μηκών των γραμμών μεταξύ τους είναι ακριβώς η τιμή του phi.
Οπτικά, αυτή η φιγούρα αρχίζει να μοιάζει με λουλούδι. Αυτό είναι αναμενόμενο γιατί στη Φύση βλέπουμε τον αριθμό 5 και την επακόλουθη σειρά Fibonacci να παίζεται σε πολλά διαφορετικά είδη λουλουδιών. Ίσως το πιο όμορφο είναι το τριαντάφυλλο.
Όλα τα βρώσιμα φυτά που φέρουν φρούτα έχουν λουλούδια με τον αριθμό των πετάλων τους με βάση το 5, ενώ οι μαργαρίτες έχουν έναν αριθμό πετάλων πάντα ίσο με έναν από τους αριθμούς της σειράς Fibonacci.
Το εσωτερικό σχήμα των βρώσιμων φρούτων βασίζεται συχνά στον αριθμό 5 και στη σειρά Fibonacci. Για παράδειγμα, ένας πυρήνας μήλου έχει 5 τμήματα λοβού σπόρων που κάνουν σχεδόν ένα τέλειο πεντάγραμμο.
Εφευρέτης αντιγράφει την αποτελεσματικότητα της φύσης
Ένα άρθρο του Kelpie Wilson που συζητά το ετήσιο συνέδριο Bioneers στο San Raphael της Καλιφόρνια, τόνισε μια εφεύρεση που έγινε κατ' εικόνα της σπείρας Fibonacci. Ο Wilson ανέφερε:
«Ο εφευρέτης Jay Harman παρουσίασε μια οικογένεια σχεδίων για ανεμιστήρες και πτερωτές με βάση τις φυσικές σπείρες που βρίσκονται στα κοχύλια και τα άνθη. Το αγαπημένο μου ήταν ένα μίξερ για γιγαντιαίες δημοτικές δεξαμενές νερού. Όταν το νερό αποθηκεύεται για μεγάλα χρονικά διαστήματα, μπορεί να παραμείνει στάσιμο και να γίνει ανθυγιεινό. Το μίξερ του Harman είναι μικροσκοπικό, μόλις μεγαλύτερο από τη γροθιά μου. Γυρίζοντας στη μέση της δεξαμενής, τίποτα δεν συμβαίνει στην αρχή, αλλά με την πάροδο του χρόνου δημιουργεί μια φυσική δίνη στη δεξαμενή που διατηρεί το νερό κυκλοφορούν και φρέσκο. Ο Harman είπε ότι ακόμα κι αν σταματήσετε το μίξερ, η δίνη θα συνεχίσει να περιστρέφεται για μέρες.
Αυτό το άρθρο δημοσιεύθηκε στο New Dawn 157.
**Τό ιστολόγιο δέν συμφωνει απαραίτητα με τις απόψεις των αρθρογράφων






Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου