—του Γιώργου Θεοχάρη—

 Εκεί, λοιπόν, γεννήθηκε, έζησε και πέθανε ο Καντ. Οι βιογράφοι του επισημαίνουν ότι ποτέ δεν απομακρύνθηκε πάνω από 16 χιλιόμετρα από την πόλη του. Γενικά, ο Καντ έζησε μία πολύ ήσυχη και μετρημένη ζωή. Ήταν τέρας αυτοπειθαρχίας: ακολουθούσε την καθημερινή του ρουτίνα με τέτοια ακρίβεια που οι κάτοικοι της πόλης διόρθωναν τα ρολόγια τους σύμφωνα με τον καθημερινό του περίπατο, καθώς έβγαινε για βόλτα την ίδια ακριβώς ώρα κάθε απόγευμα. Ο ίδιος έλεγε ότι μόνο μία φορά στη ζωή του άργησε να βγει, γιατί τον είχε συνεπάρει η ανάγνωση του Candide (1759) του Βολταίρου και ξεχάστηκε.
Εκεί, λοιπόν, γεννήθηκε, έζησε και πέθανε ο Καντ. Οι βιογράφοι του επισημαίνουν ότι ποτέ δεν απομακρύνθηκε πάνω από 16 χιλιόμετρα από την πόλη του. Γενικά, ο Καντ έζησε μία πολύ ήσυχη και μετρημένη ζωή. Ήταν τέρας αυτοπειθαρχίας: ακολουθούσε την καθημερινή του ρουτίνα με τέτοια ακρίβεια που οι κάτοικοι της πόλης διόρθωναν τα ρολόγια τους σύμφωνα με τον καθημερινό του περίπατο, καθώς έβγαινε για βόλτα την ίδια ακριβώς ώρα κάθε απόγευμα. Ο ίδιος έλεγε ότι μόνο μία φορά στη ζωή του άργησε να βγει, γιατί τον είχε συνεπάρει η ανάγνωση του Candide (1759) του Βολταίρου και ξεχάστηκε.
 Ο Όιλερ θεωρείται δικαίως ένας από τους μεγαλύτερους μαθηματικούς όλων των εποχών (παρέα με τον Αρχιμήδη, τον Γκάους και τον Νεύτωνα). Άφησε καθοριστικό έργο στον απειροστικό λογισμό και τη μαθηματική ανάλυση (αλλά και στη μηχανική, τη ρευστοδυναμική, την οπτική και την αστρονομία). Ήταν επίσης παραγωγικότατος, αφήνοντας πίσω του έργο που εκτείνεται σε περίπου 60.000 σελίδες. Ακόμα και τυφλός από το 1756, συνέχισε απτόητος και υπαγόρευε μαθηματικά στους γραμματείς του. Σκεφτόταν μαθηματικά. Με μια λέξη: χαρισματικός.
Ο Όιλερ θεωρείται δικαίως ένας από τους μεγαλύτερους μαθηματικούς όλων των εποχών (παρέα με τον Αρχιμήδη, τον Γκάους και τον Νεύτωνα). Άφησε καθοριστικό έργο στον απειροστικό λογισμό και τη μαθηματική ανάλυση (αλλά και στη μηχανική, τη ρευστοδυναμική, την οπτική και την αστρονομία). Ήταν επίσης παραγωγικότατος, αφήνοντας πίσω του έργο που εκτείνεται σε περίπου 60.000 σελίδες. Ακόμα και τυφλός από το 1756, συνέχισε απτόητος και υπαγόρευε μαθηματικά στους γραμματείς του. Σκεφτόταν μαθηματικά. Με μια λέξη: χαρισματικός.
 Δεν παραδίδεται αν ο Όιλερ έκανε ποτέ με τα πόδια τη διαδρομή. Το σίγουρο είναι ότι η βόλτα δεν θα τον βοηθούσε να βρει τη λύση. Εκείνο που χρειάστηκε ήταν ένας απλούστατος χάρτης των τεσσάρων κομματιών γης και των εφτά γεφυρών που τα ενώνουν. Κοιτώντας τον χάρτη, συνειδητοποίησε ότι μπορούσε να τον απλοποιήσει ακόμα περισσότερο, αντικαθιστώντας τα κομμάτια γης με σημεία και τις γέφυρες με γραμμές (που ενώνουν τα σημεία). Έχοντας τώρα ένα σαφές και απλούστατο γράφημα μπροστά του, έκανε μία σκέψη που δεν ήταν τίποτα για κάποιον με τις δικές του αναλυτικές ικανότητες: το πρόβλημα πλέον ισοδυναμούσε με τον σχεδιασμό επί χάρτου μιας μονοκοντυλιάς, με το μολύβι να περνάει μόνο μία φορά από κάθε “γέφυρα”. Αν το δοκιμάσετε, μετά από κάμποσες σελίδες χαρτί και ίσως ένα ολόκληρο μολύβι, θα διαπιστώσετε ότι κάτι τέτοιο είναι ανέφικτο. Δεν υπάρχει λύση.
Δεν παραδίδεται αν ο Όιλερ έκανε ποτέ με τα πόδια τη διαδρομή. Το σίγουρο είναι ότι η βόλτα δεν θα τον βοηθούσε να βρει τη λύση. Εκείνο που χρειάστηκε ήταν ένας απλούστατος χάρτης των τεσσάρων κομματιών γης και των εφτά γεφυρών που τα ενώνουν. Κοιτώντας τον χάρτη, συνειδητοποίησε ότι μπορούσε να τον απλοποιήσει ακόμα περισσότερο, αντικαθιστώντας τα κομμάτια γης με σημεία και τις γέφυρες με γραμμές (που ενώνουν τα σημεία). Έχοντας τώρα ένα σαφές και απλούστατο γράφημα μπροστά του, έκανε μία σκέψη που δεν ήταν τίποτα για κάποιον με τις δικές του αναλυτικές ικανότητες: το πρόβλημα πλέον ισοδυναμούσε με τον σχεδιασμό επί χάρτου μιας μονοκοντυλιάς, με το μολύβι να περνάει μόνο μία φορά από κάθε “γέφυρα”. Αν το δοκιμάσετε, μετά από κάμποσες σελίδες χαρτί και ίσως ένα ολόκληρο μολύβι, θα διαπιστώσετε ότι κάτι τέτοιο είναι ανέφικτο. Δεν υπάρχει λύση.
 Σύμφωνοι, αλλά ούτε αυτή ήταν απόδειξη. Αυτό το ήξεραν και οι κάτοικοι που είχαν λιώσει στο περπάτημα πάνω στις γέφυρες. Το ερώτημα που έπρεπε να απαντηθεί ήταν γιατί δεν υπήρχε λύση. Εδώ ο Όιλερ σκέφτηκε με τρόπο που δικαιολογεί τη θέση του στην ιεραρχία της ιστορίας των επιστημών. Καταρχάς, συνειδητοποίησε ότι για να υπάρχει λύση, θα πρέπει κάθε σημείο (κομμάτι γης) να συνδέεται με δύο γραμμές (γέφυρες), μία να καταλήγει και μία άλλη να ξεκινάει από αυτό. Μέχρι εδώ, εντάξει, περίπου αυτονόητο. Τώρα όμως αρχίζουν τα δύσκολα. Αν “ξαναπερνούσες” (με τα πόδια ή το μολύβι, αδιάφορο) από το ίδιο δεδομένο σημείο, θα έπρεπε και πάλι να υπάρχει μία γραμμή από και μία άλλη προς αυτό. Με άλλα λόγια, ο αριθμός των γραμμών που περνούν από κάθε σημείο πρέπει σε κάθε περίπτωση να είναι ζυγός (με την εξαίρεση των σημείων της εκκίνησης και του τερματισμού του “περίπατου”, από τα οποία, αντιστοίχως, μόνο μία γραμμή ξεκινάει και μόνο μία γραμμή καταλήγει). Κατά συνέπεια, για να υπάρχει λύση, πρέπει όλα τα σημεία να έχουν ζυγό αριθμό γραμμών, και μόνο δύο σημεία (της εκκίνησης και του τερματισμού) να έχουν μονό αριθμό γραμμών. Μετρώντας όμως το γράφημα των Εφτά Γεφυρών του Κένιγκσμπεργκ, διαπιστώνουμε ότι και τα τέσσερα σημεία έχουν μονό αριθμό γραμμών (τρία από αυτά έχουν 3 γραμμές και το τέταρτο 5). Άρα, δεν μπορεί να περάσει κανείς και από τις εφτά γέφυρες, έχοντας διασχίσει την καθεμιά από αυτές μία και μόνη φορά. Το πρόβλημα δεν έχει λύση. Ο.Ε.Δ.
Σύμφωνοι, αλλά ούτε αυτή ήταν απόδειξη. Αυτό το ήξεραν και οι κάτοικοι που είχαν λιώσει στο περπάτημα πάνω στις γέφυρες. Το ερώτημα που έπρεπε να απαντηθεί ήταν γιατί δεν υπήρχε λύση. Εδώ ο Όιλερ σκέφτηκε με τρόπο που δικαιολογεί τη θέση του στην ιεραρχία της ιστορίας των επιστημών. Καταρχάς, συνειδητοποίησε ότι για να υπάρχει λύση, θα πρέπει κάθε σημείο (κομμάτι γης) να συνδέεται με δύο γραμμές (γέφυρες), μία να καταλήγει και μία άλλη να ξεκινάει από αυτό. Μέχρι εδώ, εντάξει, περίπου αυτονόητο. Τώρα όμως αρχίζουν τα δύσκολα. Αν “ξαναπερνούσες” (με τα πόδια ή το μολύβι, αδιάφορο) από το ίδιο δεδομένο σημείο, θα έπρεπε και πάλι να υπάρχει μία γραμμή από και μία άλλη προς αυτό. Με άλλα λόγια, ο αριθμός των γραμμών που περνούν από κάθε σημείο πρέπει σε κάθε περίπτωση να είναι ζυγός (με την εξαίρεση των σημείων της εκκίνησης και του τερματισμού του “περίπατου”, από τα οποία, αντιστοίχως, μόνο μία γραμμή ξεκινάει και μόνο μία γραμμή καταλήγει). Κατά συνέπεια, για να υπάρχει λύση, πρέπει όλα τα σημεία να έχουν ζυγό αριθμό γραμμών, και μόνο δύο σημεία (της εκκίνησης και του τερματισμού) να έχουν μονό αριθμό γραμμών. Μετρώντας όμως το γράφημα των Εφτά Γεφυρών του Κένιγκσμπεργκ, διαπιστώνουμε ότι και τα τέσσερα σημεία έχουν μονό αριθμό γραμμών (τρία από αυτά έχουν 3 γραμμές και το τέταρτο 5). Άρα, δεν μπορεί να περάσει κανείς και από τις εφτά γέφυρες, έχοντας διασχίσει την καθεμιά από αυτές μία και μόνη φορά. Το πρόβλημα δεν έχει λύση. Ο.Ε.Δ.

Αυτό είναι το σημείο όπου θα πεταχτεί το κλασικό πνεύμα αντιλογίας και θα πει: «Ωραία, ο Όιλερ απέδειξε ότι οι κάτοικοι της Καινιξβέργης αδίκως έλιωναν τις σόλες τους στις γέφυρες του Πρέγκελ προσπαθώντας να διασχίσουν και τις εφτά, αλλά μία και μόνο φορά την καθεμιά. Ε, και;» Και όμως. Έχω ήδη γράψει για τη χρησιμότητα της άχρηστης γνώσης, ας μην επανέλθω. Να πω όμως για τις συνέπειες αυτής της απόδειξης και μόνο. Κατά πρώτον, θεμελίωσε έναν τομέα των Εφαρμοσμένων Μαθηματικών, τη Θεωρία των Γραφημάτων, η χρησιμότητα της οποίας δεν φαντάζομαι να αμφισβητείται (ο χάρτης του μετρό που λέγαμε πριν είναι ένα μόνο από τα πάμπολλα παραδείγματα) και άνοιξε τον δρόμο για την Τοπολογία.

Στον Όιλερ οφείλουμε το πρώτο θεώρημα της Θεωρίας των Γραφημάτων (ναι, αυτό με τις Γέφυρες), απ’ όπου προέκυψε, η χαρακτηριστική Όιλερ-Πουανκαρέ της Αλγεβρικής Τοπολογίας: μία σταθερά που περιγράφει το σχήμα ενός τοπολογικού χώρου (αρχικά: ενός πολύεδρου) ή τη δομή αυτού, ανεξάρτητα από τον τρόπο κλίσης του. Η σταθερά προκύπτει από τον τύπο:
Αν κοιτάξετε σε κάποια παλιά εγκυκλοπαίδεια το λήμμα “Καντ”, θα διαβάσετε ότι ο μεγάλος γερμανός φιλόσοφος Ιμμάνουελ Καντ (1724-1804) γεννήθηκε στην Καινιξβέργη της Ανατολικής Πρωσίας. Πόλη με αυτό το όνομα, όμως, σε σύγχρονο χάρτη δεν θα βρείτε. Έτσι είχαμε εξελληνίσει το Κένιγκσμπεργκ (Königsberg), το οποίο επίσης δεν υπάρχει σήμερα ως όνομα. Πολύπαθη πόλη.

Μέχρι το 1255, στην περιοχή βρισκόταν ένα πρωσικό φρούριο, το Twangste. Το 1255, κατά τη διάρκεια των Βόρειων Σταυροφοριών, οι Τεύτονες Ιππότες έχτισαν στην ίδια τοποθεσία ένα νέο φρούριο, το οποίο ονόμασαν Κένιγκσμπεργκ (“το Βουνό του Βασιλιά”, στα κάτω γερμανικά). Έκτοτε, η πόλη ήταν, διαδοχικά, τμήμα του Κράτους του Τευτονικού Τάγματος, της Πολωνο-Λιθουανικής Κοινοπολιτείας, της Ρωσικής Αυτοκρατορίας, της Πρωσίας και της Γερμανίας (έως το 1945). Λίγο πριν από το τέλος του Β΄ Παγκοσμίου Πολέμου, η πόλη καταστράφηκε σχεδόν ολοκληρωτικά από τους βομβαρδισμούς των Συμμάχων. Το 1945, την κατέλαβε ο Κόκκινος Στρατός και ο γερμανικός πληθυσμός διέφυγε ή εκδιώχθηκε. Το 1946, μετονομάστηκε σε Καλίνινγκραντ, προς τιμή τού Μιχαήλ Καλίνιν, Προέδρου του Προεδρείου του Ανωτάτου Σοβιέτ της ΕΣΣΔ, που είχε μόλις πεθάνει. Έτσι λέγεται και σήμερα, καθώς ανήκει στη Ρωσία, παρότι είναι γεωγραφικά αποκομμένη από αυτήν: βρίσκεται στον ρωσικό θύλακα μεταξύ Πολωνίας και Λιθουανίας, πάνω στη Βαλτική.
 Εκεί, λοιπόν, γεννήθηκε, έζησε και πέθανε ο Καντ. Οι βιογράφοι του επισημαίνουν ότι ποτέ δεν απομακρύνθηκε πάνω από 16 χιλιόμετρα από την πόλη του. Γενικά, ο Καντ έζησε μία πολύ ήσυχη και μετρημένη ζωή. Ήταν τέρας αυτοπειθαρχίας: ακολουθούσε την καθημερινή του ρουτίνα με τέτοια ακρίβεια που οι κάτοικοι της πόλης διόρθωναν τα ρολόγια τους σύμφωνα με τον καθημερινό του περίπατο, καθώς έβγαινε για βόλτα την ίδια ακριβώς ώρα κάθε απόγευμα. Ο ίδιος έλεγε ότι μόνο μία φορά στη ζωή του άργησε να βγει, γιατί τον είχε συνεπάρει η ανάγνωση του Candide (1759) του Βολταίρου και ξεχάστηκε.
Εκεί, λοιπόν, γεννήθηκε, έζησε και πέθανε ο Καντ. Οι βιογράφοι του επισημαίνουν ότι ποτέ δεν απομακρύνθηκε πάνω από 16 χιλιόμετρα από την πόλη του. Γενικά, ο Καντ έζησε μία πολύ ήσυχη και μετρημένη ζωή. Ήταν τέρας αυτοπειθαρχίας: ακολουθούσε την καθημερινή του ρουτίνα με τέτοια ακρίβεια που οι κάτοικοι της πόλης διόρθωναν τα ρολόγια τους σύμφωνα με τον καθημερινό του περίπατο, καθώς έβγαινε για βόλτα την ίδια ακριβώς ώρα κάθε απόγευμα. Ο ίδιος έλεγε ότι μόνο μία φορά στη ζωή του άργησε να βγει, γιατί τον είχε συνεπάρει η ανάγνωση του Candide (1759) του Βολταίρου και ξεχάστηκε.
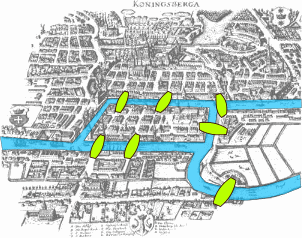
Δεν ξέρω αν ο καθημερινός περίπατος του Καντ περιλάμβανε τις διάσημες Εφτά Γέφυρες του Κένιγκσμπεργκ, από τη διάταξη των οποίων προέκυψε ένα πρόβλημα που απασχολούσε για αιώνες τους κατοίκους της πόλης. Κατά τη διάρκεια του 18ου αιώνα, όταν το Κένιγκσμπεργκ ήταν μέρος της αυτοκρατορικής Ρωσίας, υπήρχαν εφτά γέφυρες που ένωναν τις δύο όχθες του ποταμού Πρέγκελ, ο οποίος διασχίζει την πόλη, και τα δύο νησάκια μέσα στον ποταμό. Αναμφίβολα θα ήταν ωραία η διαδρομή πάνω από τις γέφυρες για να την επιλέγουν οι κάτοικοι για τον απογευματινό τους περίπατο. Το αγαπημένο τους παιχνίδι, το οποίο δεν ξέρουμε πώς ξεκίνησε, ήταν να περάσουν και τις εφτά γέφυρες, διασχίζοντας μόνο μία φορά την καθεμιά. Δεν ήταν απαραίτητο το σημείο εκκίνησης να ταυτίζεται με το σημείο τερματισμού· οι μόνοι περιορισμοί ήταν: περνάμε και τις εφτά γέφυρες και μόνο μία φορά την κάθε γέφυρα, από τη μία της άκρη μέχρι την άλλη (περπατώντας και όχι κολυμπώντας, δηλαδή). Ποτέ δεν τα κατάφεραν: όποια διαδρομή κι αν ακολουθούσαν, πάντα υπήρχε μία γέφυρα που δεν μπορούσαν να προσεγγίσουν. Μήπως τελικά ήταν αδύνατο κάτι τέτοιο; Στο κάτω-κάτω, ο αριθμός των διαδρομών ήταν πεπερασμένος. Συνεπώς, αν υπήρχε τρόπος, θα είχε βρεθεί με τόσα πέρα-δώθε ανά τους αιώνες. Κάθε τόσο βρισκόταν κάποιος που ισχυριζόταν ότι τα είχε καταφέρει, αλλά όταν του ζητούσαν να τους αναπαραστήσει τη διαδρομή, η κατάληξη ήταν η συνήθης: μία γέφυρα παρέμενε απροσπέλαστη. Μάλλον δεν υπήρχε τρόπος. Όμως, αυτό το “μάλλον” ήταν που τους καθόταν στραβά. Άλλο εικασία κι άλλο απόδειξη. Ανάμεσά τους είναι που κάνει πάρτι η επιστήμη. Χρειάστηκε η ιδιοφυία του Ελβετού μαθηματικού Λέοναρντ Όιλερ (1707-1783) για να αποδειχτεί ότι το πρόβλημα είναι όντως άλυτο.
 Ο Όιλερ θεωρείται δικαίως ένας από τους μεγαλύτερους μαθηματικούς όλων των εποχών (παρέα με τον Αρχιμήδη, τον Γκάους και τον Νεύτωνα). Άφησε καθοριστικό έργο στον απειροστικό λογισμό και τη μαθηματική ανάλυση (αλλά και στη μηχανική, τη ρευστοδυναμική, την οπτική και την αστρονομία). Ήταν επίσης παραγωγικότατος, αφήνοντας πίσω του έργο που εκτείνεται σε περίπου 60.000 σελίδες. Ακόμα και τυφλός από το 1756, συνέχισε απτόητος και υπαγόρευε μαθηματικά στους γραμματείς του. Σκεφτόταν μαθηματικά. Με μια λέξη: χαρισματικός.
Ο Όιλερ θεωρείται δικαίως ένας από τους μεγαλύτερους μαθηματικούς όλων των εποχών (παρέα με τον Αρχιμήδη, τον Γκάους και τον Νεύτωνα). Άφησε καθοριστικό έργο στον απειροστικό λογισμό και τη μαθηματική ανάλυση (αλλά και στη μηχανική, τη ρευστοδυναμική, την οπτική και την αστρονομία). Ήταν επίσης παραγωγικότατος, αφήνοντας πίσω του έργο που εκτείνεται σε περίπου 60.000 σελίδες. Ακόμα και τυφλός από το 1756, συνέχισε απτόητος και υπαγόρευε μαθηματικά στους γραμματείς του. Σκεφτόταν μαθηματικά. Με μια λέξη: χαρισματικός.
Ο Όιλερ πέρασε μεγάλο μέρος της ζωής του στην Αγία Πετρούπολη, όπου και άκουσε για πρώτη φορά το πρόβλημα με τις Εφτά Γέφυρες του Κένιγκσμπεργκ. Του Ελβετού πολύ του άρεσαν κάτι τέτοια. Όπως θα περίμενε κανείς, αντιμετώπισε τον γρίφο όπως ήξερε: με τα μαθηματικά. Και κατάφερε το 1736 να αποδείξει ότι το πρόβλημα δεν έχει λύση.

Το πρώτο βήμα προς την απόδειξη ο Όιλερ το έκανε αποσυνδέοντας τα πραγματολογικά στοιχεία (διαστάσεις, αποστάσεις, προσανατολισμό, τοπογραφία) της περιοχής από το ίδιο το πρόβλημα. Σκέφτηκε πολύ λογικά (και απολύτως αφαιρετικά) ότι αυτό που έχει σημασία ήταν το δίκτυο των γεφυρών και το πώς αυτές συνδέουν τα τέσσερα (2 όχθες, 2 νησάκια) διακριτά κομμάτια γης. Για να καταλάβετε πόσο σημαντική ήταν αυτή η ιδέα, θυμηθείτε τον χάρτη με τους σταθμούς του μετρό της Αθήνας που βρίσκεται πάνω από κάθε πόρτα σε κάθε βαγόνι. Προφανώς δεν πρόκειται για ρεαλιστική απεικόνιση της Αθήνας. Το ζητούμενο ενός τέτοιου χάρτη δεν είναι πραγματολογικό, αλλά λειτουργικό: μας δείχνει πώς συνδέονται οι σταθμοί των τριών γραμμών μεταξύ τους· μας παρέχει πληροφορίες ειδικού σκοπού· μας δίνει μια γενική εποπτεία του δικτύου.
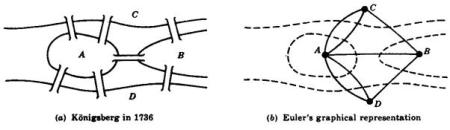
 Δεν παραδίδεται αν ο Όιλερ έκανε ποτέ με τα πόδια τη διαδρομή. Το σίγουρο είναι ότι η βόλτα δεν θα τον βοηθούσε να βρει τη λύση. Εκείνο που χρειάστηκε ήταν ένας απλούστατος χάρτης των τεσσάρων κομματιών γης και των εφτά γεφυρών που τα ενώνουν. Κοιτώντας τον χάρτη, συνειδητοποίησε ότι μπορούσε να τον απλοποιήσει ακόμα περισσότερο, αντικαθιστώντας τα κομμάτια γης με σημεία και τις γέφυρες με γραμμές (που ενώνουν τα σημεία). Έχοντας τώρα ένα σαφές και απλούστατο γράφημα μπροστά του, έκανε μία σκέψη που δεν ήταν τίποτα για κάποιον με τις δικές του αναλυτικές ικανότητες: το πρόβλημα πλέον ισοδυναμούσε με τον σχεδιασμό επί χάρτου μιας μονοκοντυλιάς, με το μολύβι να περνάει μόνο μία φορά από κάθε “γέφυρα”. Αν το δοκιμάσετε, μετά από κάμποσες σελίδες χαρτί και ίσως ένα ολόκληρο μολύβι, θα διαπιστώσετε ότι κάτι τέτοιο είναι ανέφικτο. Δεν υπάρχει λύση.
Δεν παραδίδεται αν ο Όιλερ έκανε ποτέ με τα πόδια τη διαδρομή. Το σίγουρο είναι ότι η βόλτα δεν θα τον βοηθούσε να βρει τη λύση. Εκείνο που χρειάστηκε ήταν ένας απλούστατος χάρτης των τεσσάρων κομματιών γης και των εφτά γεφυρών που τα ενώνουν. Κοιτώντας τον χάρτη, συνειδητοποίησε ότι μπορούσε να τον απλοποιήσει ακόμα περισσότερο, αντικαθιστώντας τα κομμάτια γης με σημεία και τις γέφυρες με γραμμές (που ενώνουν τα σημεία). Έχοντας τώρα ένα σαφές και απλούστατο γράφημα μπροστά του, έκανε μία σκέψη που δεν ήταν τίποτα για κάποιον με τις δικές του αναλυτικές ικανότητες: το πρόβλημα πλέον ισοδυναμούσε με τον σχεδιασμό επί χάρτου μιας μονοκοντυλιάς, με το μολύβι να περνάει μόνο μία φορά από κάθε “γέφυρα”. Αν το δοκιμάσετε, μετά από κάμποσες σελίδες χαρτί και ίσως ένα ολόκληρο μολύβι, θα διαπιστώσετε ότι κάτι τέτοιο είναι ανέφικτο. Δεν υπάρχει λύση. Σύμφωνοι, αλλά ούτε αυτή ήταν απόδειξη. Αυτό το ήξεραν και οι κάτοικοι που είχαν λιώσει στο περπάτημα πάνω στις γέφυρες. Το ερώτημα που έπρεπε να απαντηθεί ήταν γιατί δεν υπήρχε λύση. Εδώ ο Όιλερ σκέφτηκε με τρόπο που δικαιολογεί τη θέση του στην ιεραρχία της ιστορίας των επιστημών. Καταρχάς, συνειδητοποίησε ότι για να υπάρχει λύση, θα πρέπει κάθε σημείο (κομμάτι γης) να συνδέεται με δύο γραμμές (γέφυρες), μία να καταλήγει και μία άλλη να ξεκινάει από αυτό. Μέχρι εδώ, εντάξει, περίπου αυτονόητο. Τώρα όμως αρχίζουν τα δύσκολα. Αν “ξαναπερνούσες” (με τα πόδια ή το μολύβι, αδιάφορο) από το ίδιο δεδομένο σημείο, θα έπρεπε και πάλι να υπάρχει μία γραμμή από και μία άλλη προς αυτό. Με άλλα λόγια, ο αριθμός των γραμμών που περνούν από κάθε σημείο πρέπει σε κάθε περίπτωση να είναι ζυγός (με την εξαίρεση των σημείων της εκκίνησης και του τερματισμού του “περίπατου”, από τα οποία, αντιστοίχως, μόνο μία γραμμή ξεκινάει και μόνο μία γραμμή καταλήγει). Κατά συνέπεια, για να υπάρχει λύση, πρέπει όλα τα σημεία να έχουν ζυγό αριθμό γραμμών, και μόνο δύο σημεία (της εκκίνησης και του τερματισμού) να έχουν μονό αριθμό γραμμών. Μετρώντας όμως το γράφημα των Εφτά Γεφυρών του Κένιγκσμπεργκ, διαπιστώνουμε ότι και τα τέσσερα σημεία έχουν μονό αριθμό γραμμών (τρία από αυτά έχουν 3 γραμμές και το τέταρτο 5). Άρα, δεν μπορεί να περάσει κανείς και από τις εφτά γέφυρες, έχοντας διασχίσει την καθεμιά από αυτές μία και μόνη φορά. Το πρόβλημα δεν έχει λύση. Ο.Ε.Δ.
Σύμφωνοι, αλλά ούτε αυτή ήταν απόδειξη. Αυτό το ήξεραν και οι κάτοικοι που είχαν λιώσει στο περπάτημα πάνω στις γέφυρες. Το ερώτημα που έπρεπε να απαντηθεί ήταν γιατί δεν υπήρχε λύση. Εδώ ο Όιλερ σκέφτηκε με τρόπο που δικαιολογεί τη θέση του στην ιεραρχία της ιστορίας των επιστημών. Καταρχάς, συνειδητοποίησε ότι για να υπάρχει λύση, θα πρέπει κάθε σημείο (κομμάτι γης) να συνδέεται με δύο γραμμές (γέφυρες), μία να καταλήγει και μία άλλη να ξεκινάει από αυτό. Μέχρι εδώ, εντάξει, περίπου αυτονόητο. Τώρα όμως αρχίζουν τα δύσκολα. Αν “ξαναπερνούσες” (με τα πόδια ή το μολύβι, αδιάφορο) από το ίδιο δεδομένο σημείο, θα έπρεπε και πάλι να υπάρχει μία γραμμή από και μία άλλη προς αυτό. Με άλλα λόγια, ο αριθμός των γραμμών που περνούν από κάθε σημείο πρέπει σε κάθε περίπτωση να είναι ζυγός (με την εξαίρεση των σημείων της εκκίνησης και του τερματισμού του “περίπατου”, από τα οποία, αντιστοίχως, μόνο μία γραμμή ξεκινάει και μόνο μία γραμμή καταλήγει). Κατά συνέπεια, για να υπάρχει λύση, πρέπει όλα τα σημεία να έχουν ζυγό αριθμό γραμμών, και μόνο δύο σημεία (της εκκίνησης και του τερματισμού) να έχουν μονό αριθμό γραμμών. Μετρώντας όμως το γράφημα των Εφτά Γεφυρών του Κένιγκσμπεργκ, διαπιστώνουμε ότι και τα τέσσερα σημεία έχουν μονό αριθμό γραμμών (τρία από αυτά έχουν 3 γραμμές και το τέταρτο 5). Άρα, δεν μπορεί να περάσει κανείς και από τις εφτά γέφυρες, έχοντας διασχίσει την καθεμιά από αυτές μία και μόνη φορά. Το πρόβλημα δεν έχει λύση. Ο.Ε.Δ.
Αυτό είναι το σημείο όπου θα πεταχτεί το κλασικό πνεύμα αντιλογίας και θα πει: «Ωραία, ο Όιλερ απέδειξε ότι οι κάτοικοι της Καινιξβέργης αδίκως έλιωναν τις σόλες τους στις γέφυρες του Πρέγκελ προσπαθώντας να διασχίσουν και τις εφτά, αλλά μία και μόνο φορά την καθεμιά. Ε, και;» Και όμως. Έχω ήδη γράψει για τη χρησιμότητα της άχρηστης γνώσης, ας μην επανέλθω. Να πω όμως για τις συνέπειες αυτής της απόδειξης και μόνο. Κατά πρώτον, θεμελίωσε έναν τομέα των Εφαρμοσμένων Μαθηματικών, τη Θεωρία των Γραφημάτων, η χρησιμότητα της οποίας δεν φαντάζομαι να αμφισβητείται (ο χάρτης του μετρό που λέγαμε πριν είναι ένα μόνο από τα πάμπολλα παραδείγματα) και άνοιξε τον δρόμο για την Τοπολογία.

Στον Όιλερ οφείλουμε το πρώτο θεώρημα της Θεωρίας των Γραφημάτων (ναι, αυτό με τις Γέφυρες), απ’ όπου προέκυψε, η χαρακτηριστική Όιλερ-Πουανκαρέ της Αλγεβρικής Τοπολογίας: μία σταθερά που περιγράφει το σχήμα ενός τοπολογικού χώρου (αρχικά: ενός πολύεδρου) ή τη δομή αυτού, ανεξάρτητα από τον τρόπο κλίσης του. Η σταθερά προκύπτει από τον τύπο:
χ = V˗E+F
όπου χ η σταθερά, V οι κορυφές, E οι ακμές και F οι έδρες δεδομένου πολύεδρου. Για τη σφαίρα και για όλα τα σφαιρικά πολύεδρα (και για τις γέφυρες του Κένιγκσμπεργκ!) χ = 2.
Κατά σύμπτωση, στην Αγία Πετρούπολη γράφτηκε η πρώτη σελίδα της Τοπολογίας (εν σπέρματι, έστω) από τον Όιλερ και η μέχρι στιγμής τελευταία –και ολόχρυση– από τον μυστήριο κύριο Πέρελμαν, με την απόδειξη της Εικασίας του Πουανκαρέ. Και όλα αυτά, επειδή οι κάτοικοι του Κένιγκσμπεργκ ήθελαν να προσθέσουν λίγη μαγεία στον περίπατό τους.
Δεν γνωρίζουμε αν ο Καντ είχε ασχοληθεί ποτέ με το πρόβλημα των Εφτά Γεφυρών (υποθέτω πως θα είχε – οι άνθρωποι που σκέφτονται δεν υπάρχει περίπτωση να αγνοήσουν οποιοδήποτε πρόβλημα, έστω και μόνο και για να κάνουν τη βόλτα τους πιο ενδιαφέρουσα). Ούτως ή άλλως, εκείνος είχε άλλα στο μυαλό του: σχεδίαζε την Κοπερνίκεια Επανάσταση στη φιλοσοφία – πού καιρός να μετράει γέφυρες; Εντούτοις, ο Όιλερ, θεμελιώνοντας τη Θεωρία των Γραφημάτων και προοικονομώντας την Τοπολογία με αφορμή τις Γέφυρες του Κένιγκσμπεργκ, προετοίμασε μια αντίστοιχη Κοπερνίκεια Επανάσταση στα μαθηματικά: άνοιξε τον δρόμο για μια νέα προσέγγιση του χώρου και της γεωμετρίας, μετατοπίζοντας το κέντρο βάρους από τα μετρήσιμα μεγέθη (διαστάσεις, αποστάσεις, γωνίες κ.λπ.) των γεωμετρικών οντοτήτων στη θαυμαστή αφαίρεση των τρόπων με τους οποίους αυτές συνδέονται μεταξύ. Και έτσι περάσαμε σε μια νέα εποχή για τα μαθηματικά, την εποχή της τοπολογίας, οι δυνατότητες και εφαρμογές της οποίας φαντάζουν σήμερα ανεξάντλητες.
Όσο για τις Εφτά Γέφυρες, τρεις από αυτές υπάρχουν ακόμα στην αυθεντική τους μορφή, άλλες δύο έχουν ανακατασκευαστεί και μόνο δύο δεν υπάρχουν πια. Αν βρεθείτε ποτέ στο σημερινό Καλίνινγκραντ, κάντε μια βόλτα στις γέφυρες: ποτέ δεν ξέρει κανείς πού του την έχει στημένη η ιδέα της ζωής του.

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου